常见简单算法归纳

ZJ Lv100
  2024-10-15 2024-10-15 Created   2025-01-17 01:35:56 2025-01-17 01:35:56 Updated      5.4k Words  19 Mins  

前言

以下将以常见基础问题的对应解答方法进行算法实例与数据结构的总结

字符串匹配

image-20241015001746389

朴素模式匹配算法（暴力解决）

原理

主串长度为n，模式串长度为 m
将主串所有长度为m的子串依次与模式串对比，直到找到一个完全匹配的子串或所有的子串都不匹配为止

最多有n-m+1个子串

代码实现

image-20241015002049555

时间复杂度

image-20241015002108960

KMP算法

原理

根据next数组，不经过回溯主串指针达到减小时间复杂度

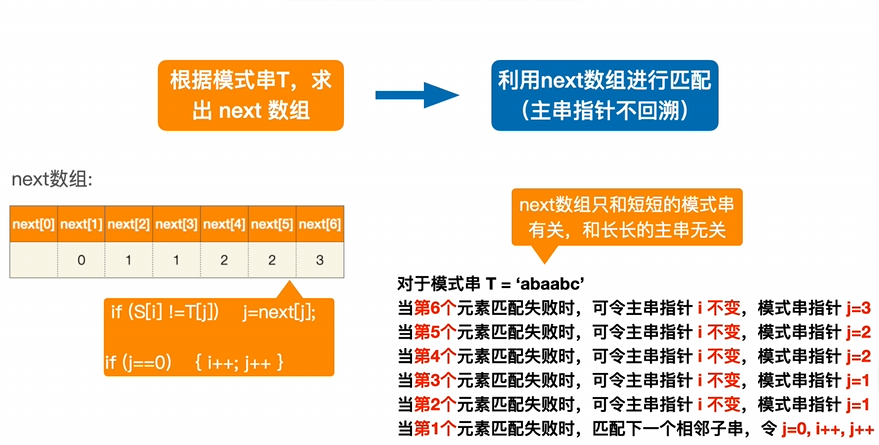
image-20241015002436924

代码实现

image-20241015002518468

求next数组

手算

根据当前字符的前端进行查找

下标j 0 1 2 3 4 5 6 7 8
模式串 a b a a b c a b a
next[j] -1 0 0 1 1 2 0 1 3

始终满足next[0]=-1;next[1]=0

计算next看前面的字符串和离自己最近的几个有相同的

next[2]看前面的”ab”，b没有和前面匹配的，则连1都没有

next[3]看前面的”aba”，a有相同的能够匹配

next[4]看前面的”abaa”，a有相同的能够匹配，但是aa没有能匹配的

next[5]看前面的”abaab”，b有相同的能够匹配，ab也有能匹配的，但aab没有能匹配的

next[6]看前面的”abaabc”，c没有能匹配的，则连1都没有

next[7]看前面的”abaabca”，a有相同的能够匹配，但是ca没有能匹配的

next[8]看前面的”abaabcab”，b有相同的能够匹配，ab也有能匹配的，但cab没有能匹配的

next[9]看前面的”abaabcaba”，a有相同的能够匹配，ba也有能匹配的，aba也有能匹配的，但caba没有能匹配的

注意：”ababa”的next值为3，后面的aba与前面的aba能够匹配

机算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void GetNext(char* t, int* next) {
    int j = 0, k = -1;
    next[0] = -1;
    int t_len = strlen(t);

    while (j < t_len - 1) {
        if (k == -1 || t[j] == t[k]) {
            j++;
            k++;
            if (t[j] != t[k])
                next[j] = k;
            else
                next[j] = next[k]; // 优化
        }
        else {
            k = next[k];
        }
    }
    // 输出next数组
    printf("next数组: ");
    for (int i = 0; i < t_len; i++) {
        printf("%d ", next[i]);
    }
    printf("\n");
}

算法优化

将next值进行替换，减少不必要的时间，得到nextval数组再进行匹配

下标j 0 1 2 3 4 5 6 7 8
模式串 a b a a b c a b a
next[j] -1 0 0 1 1 2 0 1 3
nextval[j] -1 0 -1 1 0 2 -1 0 1

从后往前看（从前往后也可以），next[8]值为3，找到j为3，若二者的模式串字符相等，则将next[8]该改为next[3]，以此类推，得到优化有的nextval数组

比较

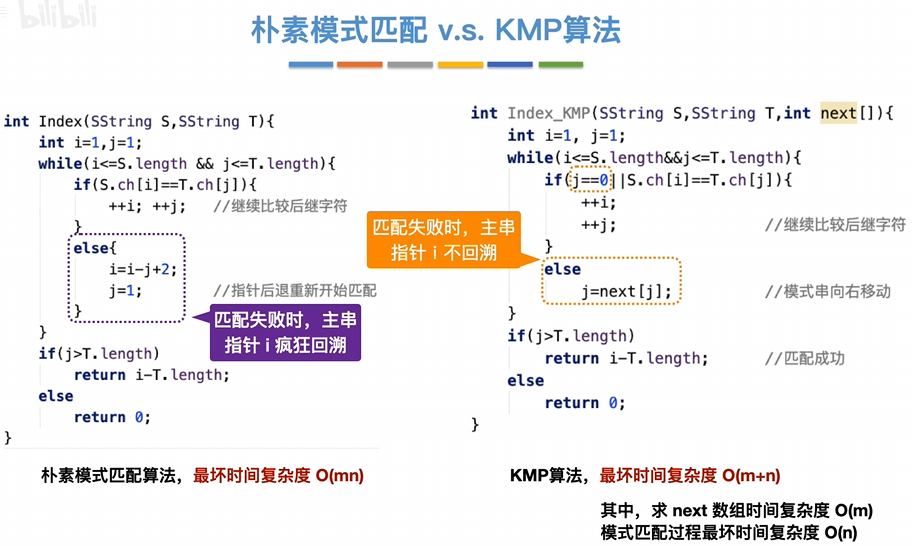
image-20241015002610032

求最小生成树

最小生成树不止一种

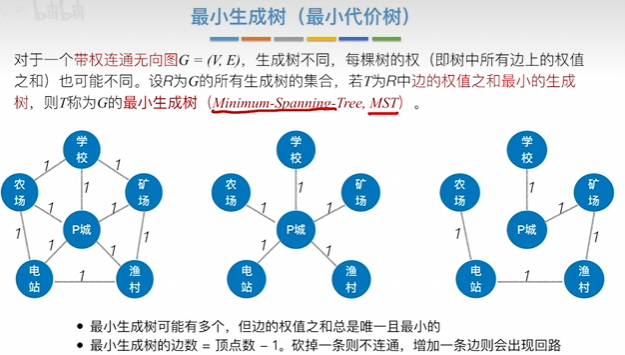
image-20241015000602373

Prim算法（普里姆算法）

简单记忆：根据节点找权值

原理

从某一个顶点开始构建生成树;每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止

理解

开始选中一点，找到距离其代价最小的顶点纳入树中，再找到这两个点的下一个最优点并纳入树中，知道全部纳入为止

图实例

1、最开始只有一个“P城”点

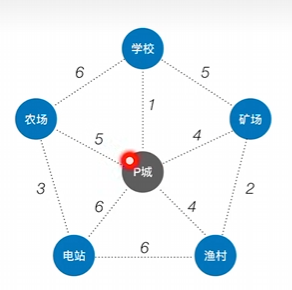
image-20241014234729896

2、找到距离其代价最小的顶点纳入树中

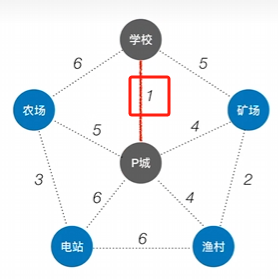
image-20241014234807642

如此往复继续查找这两个点所有代价中最小代价的点并纳入树中

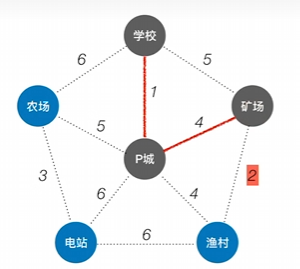
image-20241014234904830

直到最后找完即可（最小生成树不只一种）

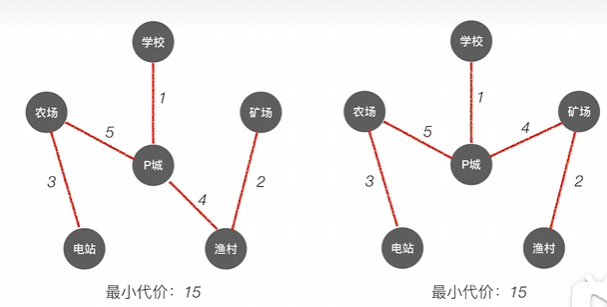
image-20241014235001262

时间复杂度

image-20241015000338410

Kruskal算法（克鲁斯卡尔算法）

简单记忆：根据权值画节点

原理

每次选择一条权值最小的边，使这条边的两头连通(原本已经连通的就不选)，直到所有结点都连通

理解

找到整个体系中权值最小的边，将该边的两头纳入树中，再选择剩下的权值最小的边将该边的两头纳入树中，如果出现一边的两头已纳入的情况则忽略该边，直到所有结点都连通

图示例

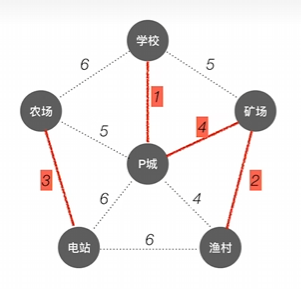
找到整个体系中权值最小的边

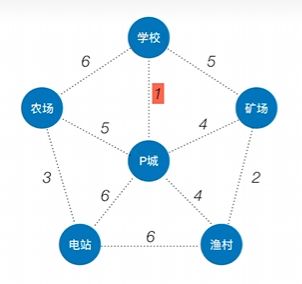
image-20241014235743359

将该边的两头纳入树中

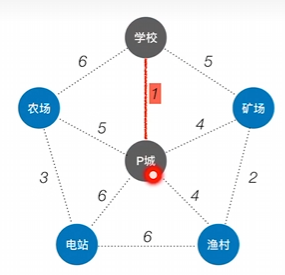
image-20241014235755337

再选择剩下的权值最小的边将该边的两头纳入树中

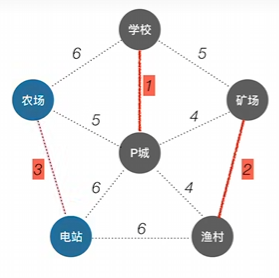
image-20241014235844715

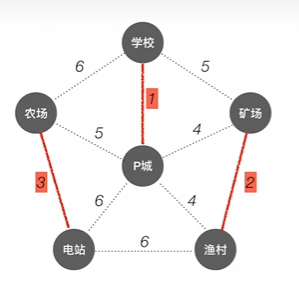
image-20241014235856083

剩余的连接需要看是否连通（间接连通也是连通了）

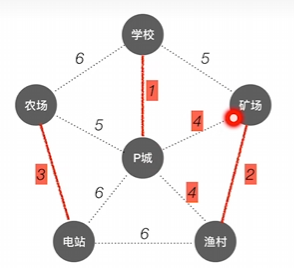
image-20241014235940173

若没有连通则进行连通

image-20241015000004968

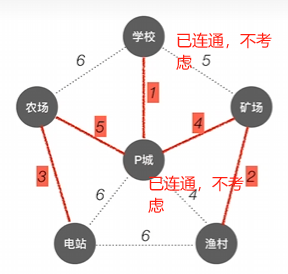
image-20241015000106584

时间复杂度

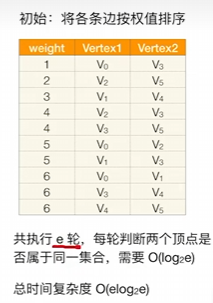
image-20241015000403547

比较

Prim算法时间复杂度为O(|V|^2^)——适合边稠密图，即|E|大的

image-20241015000338410

Kruskal算法时间复杂度为O(|E|log2|E|)——适合边稀疏图，即|E|小的

image-20241015000403547

最短路径问题

image-20241015000511989

BFS算法（广度优先算法）

无权图

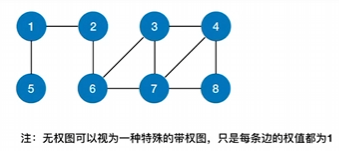
image-20241015000808214

代码实现

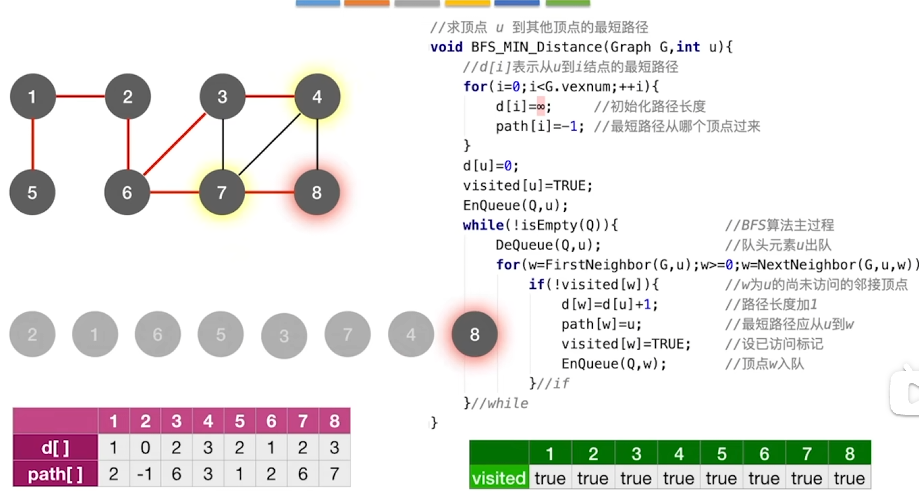
image-20241015000917252

核心思想

利用队列对图进行层次遍历，加上pre前驱指针找到最短路径

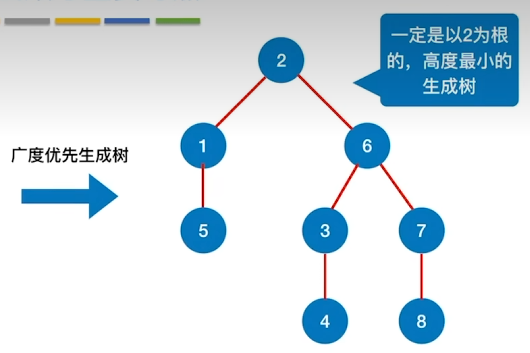
image-20241015001101608

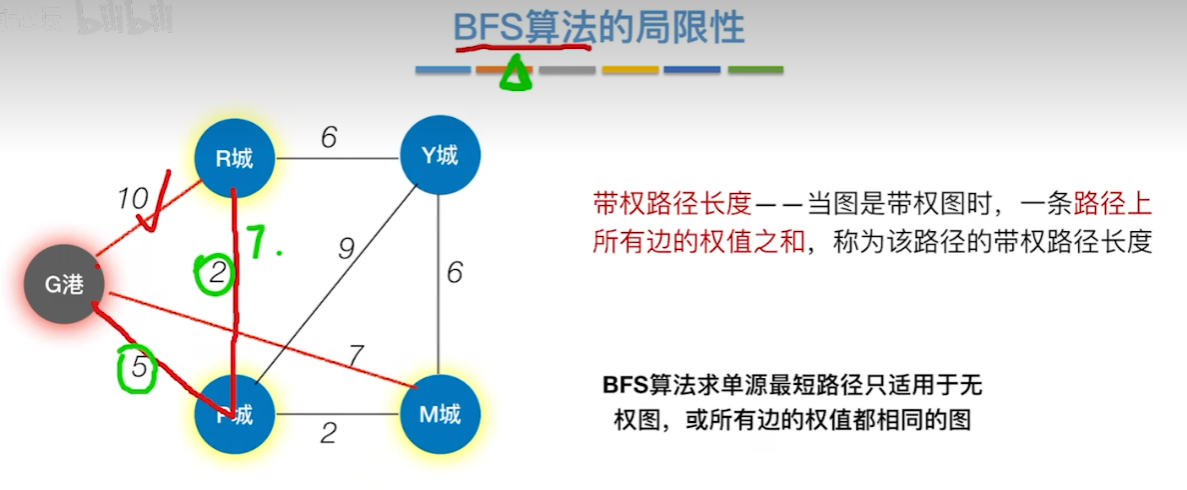
局限性

image-20241015004510040

Dijkstra算法（迪杰斯特拉算法）

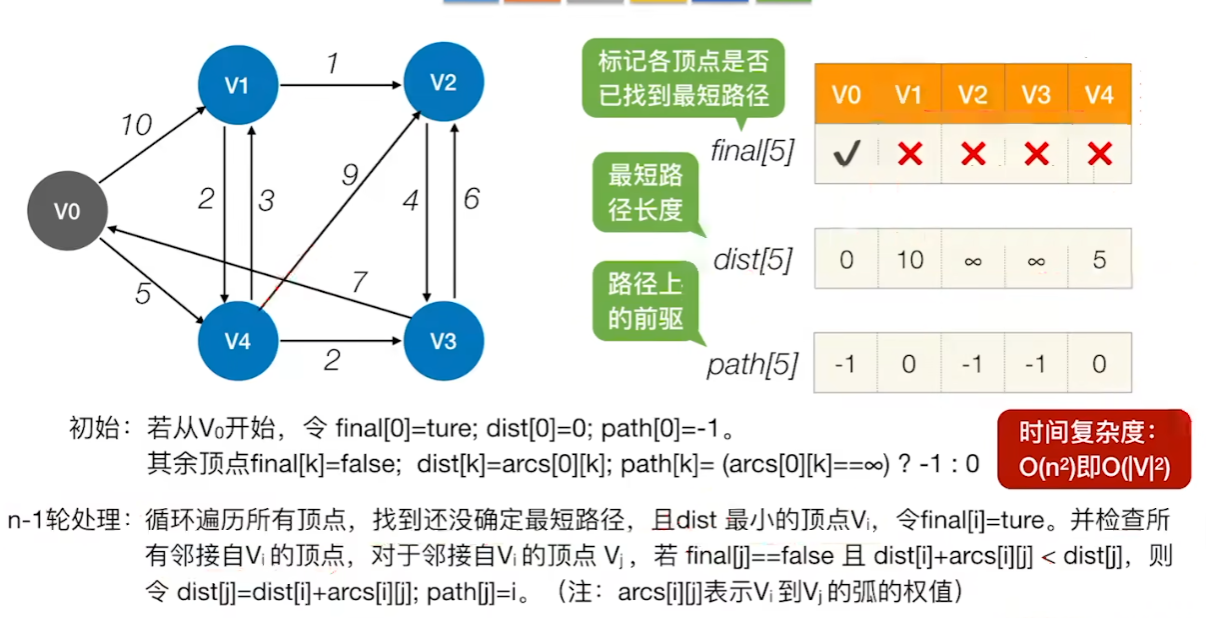
image-20241015004914940

图示例

1、初始化3个数组，最短路径找不到就存为无穷，且其前驱设为-1表示没有前驱

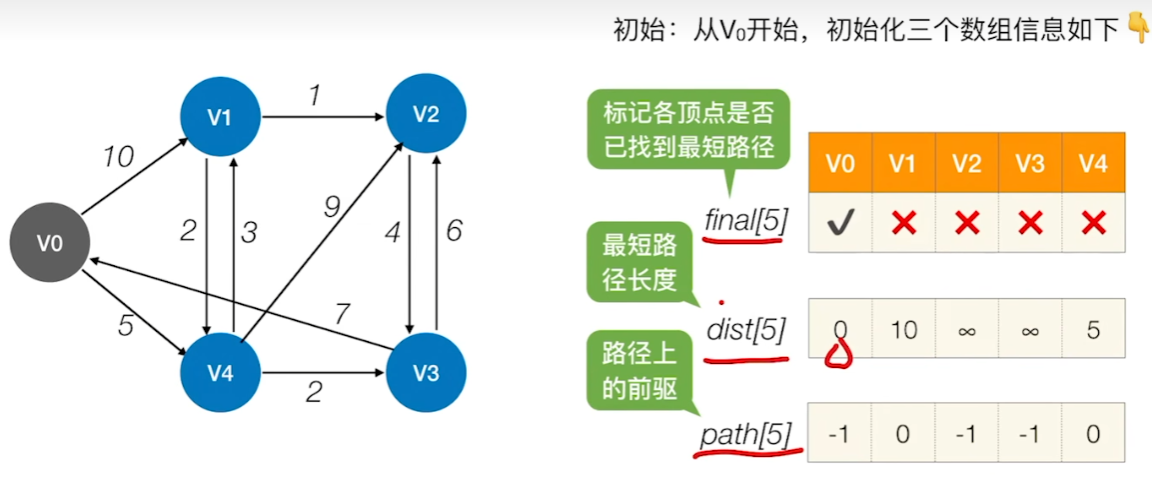
image-20241015005350067

2、遍历所有结点，找到还没有确定最短路径的点，且其dist值最小的点，将其标记为找到最短路径了

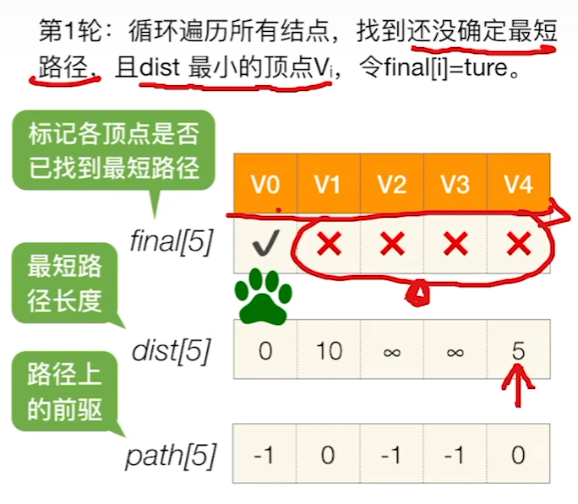
image-20241015005845139

3、检查所有邻接自V的顶点，若其 final 值为false,则更新 dist 和 path 信息

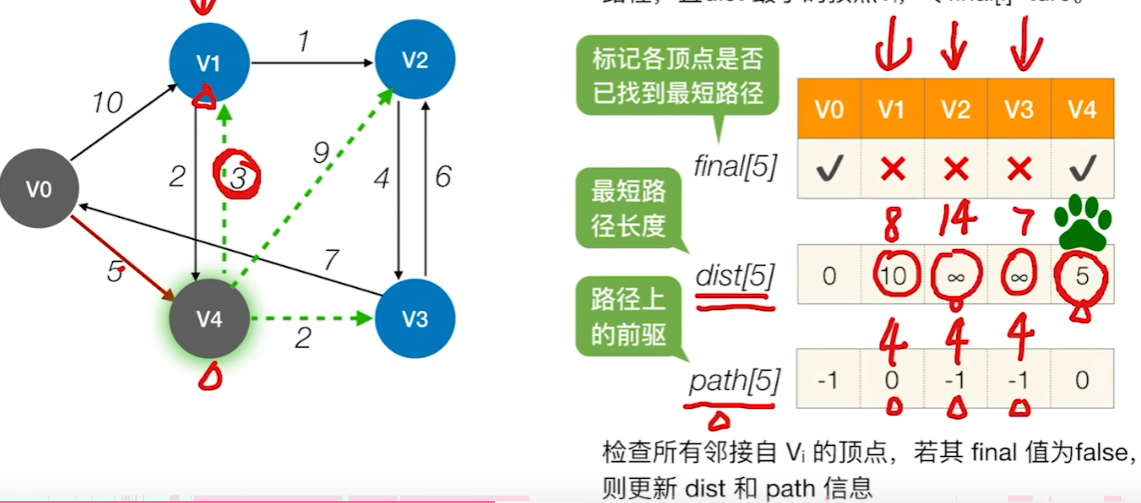
image-20241015005944334

4、遍历所有结点，找到还没有确定最短路径的点，且其dist值最小的点，将其标记为找到最短路径了

image-20241015010038493

5、检查所有邻接自V的顶点，若其 final 值为false,则更新 dist 和 path 信息

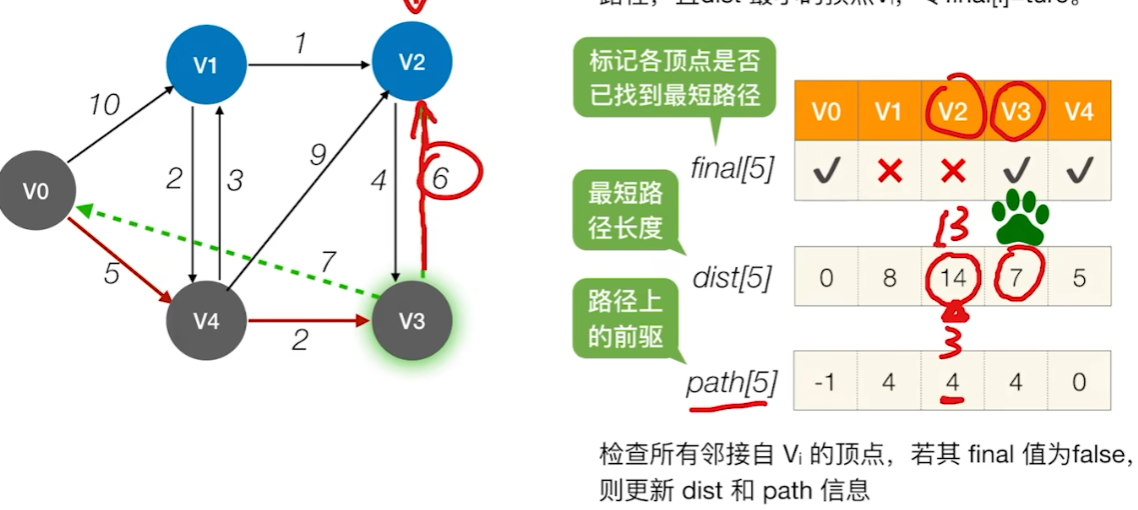
image-20241015010118386

6、遍历所有结点，找到还没有确定最短路径的点，且其dist值最小的点，将其标记为找到最短路径了

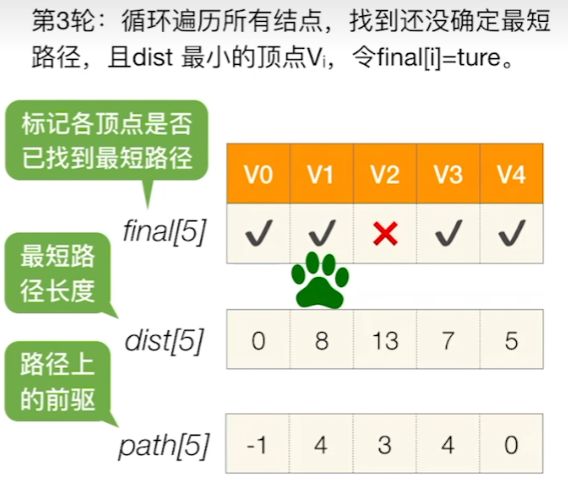
image-20241015010144200

7、检查所有邻接自V的顶点，若其 final 值为false,则更新 dist 和 path 信息

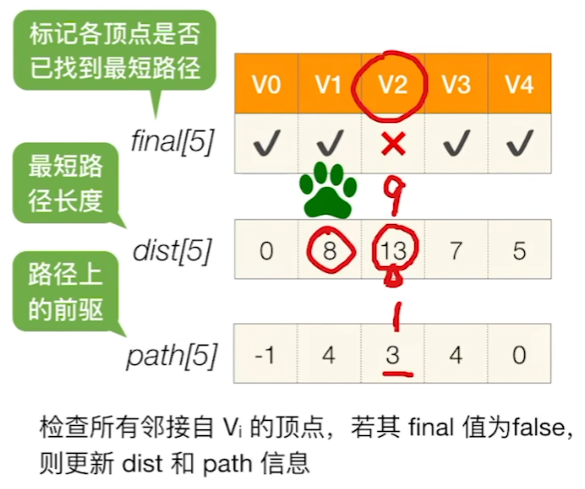
image-20241015010203220

8、遍历所有结点，找到还没有确定最短路径的点，且其dist值最小的点，将其标记为找到最短路径了

image-20241015010226097

算法结束

代码实现

image-20241015010352720

时间复杂度

与Prim算法类似

image-20241015004933257

局限性

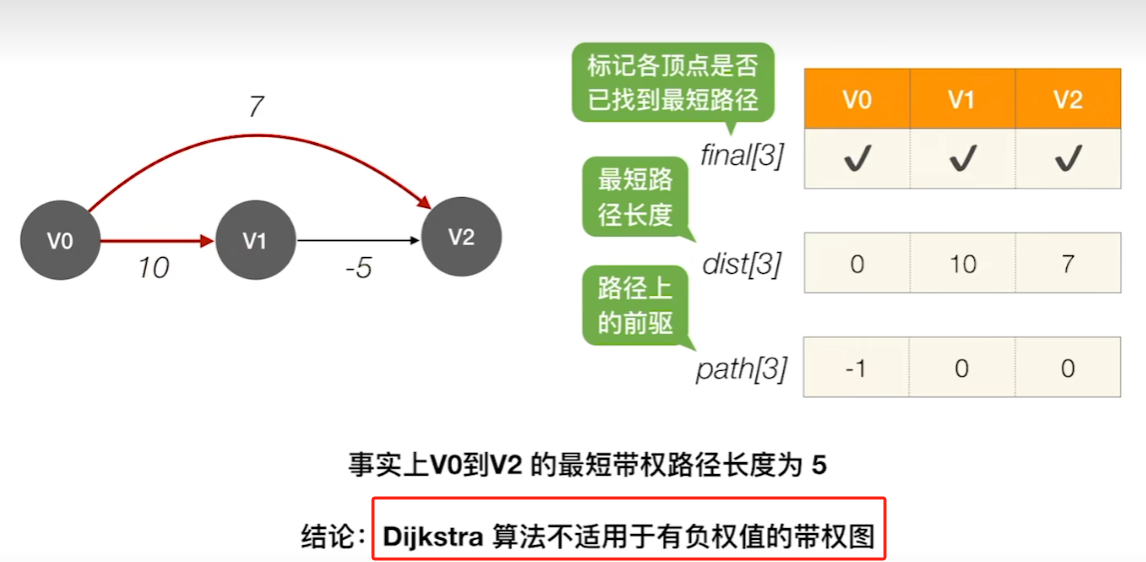
image-20241015005141879

Floyd算法（弗洛伊德算法——动态规划）

image-20241015010522668

图示例

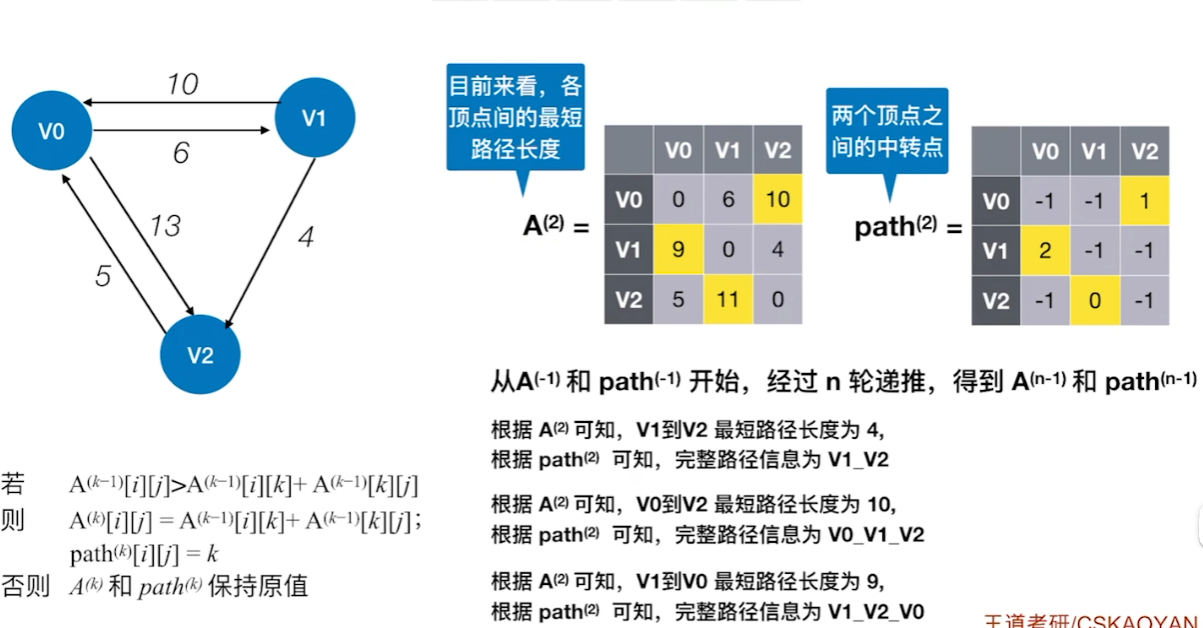
image-20241015011230339

代码实现

image-20241015011405355

时间、空间复杂度

image-20241015011426396

比较

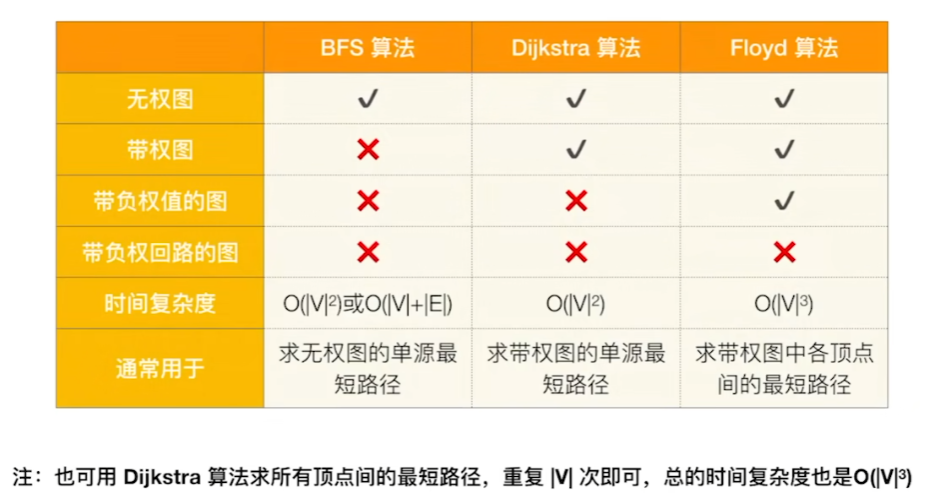
image-20241015011520661

查找算法与数据结构

ASL概念

概念

查找算法的评价指标

查找成功

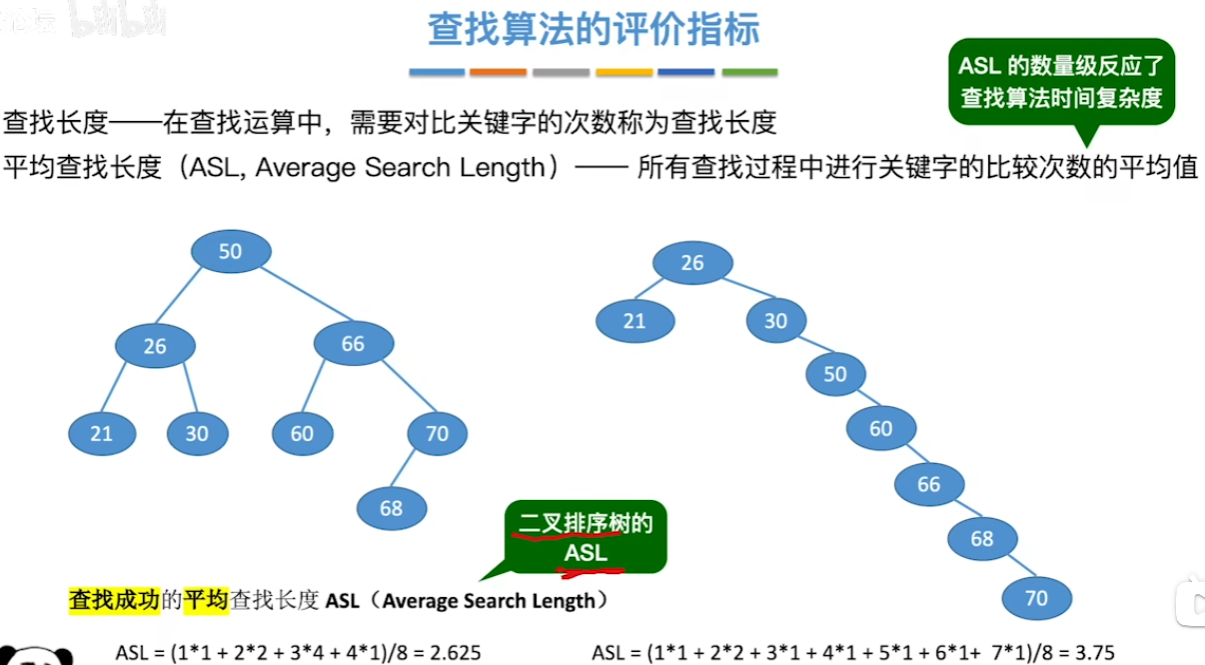
image-20241015234132897

查找失败

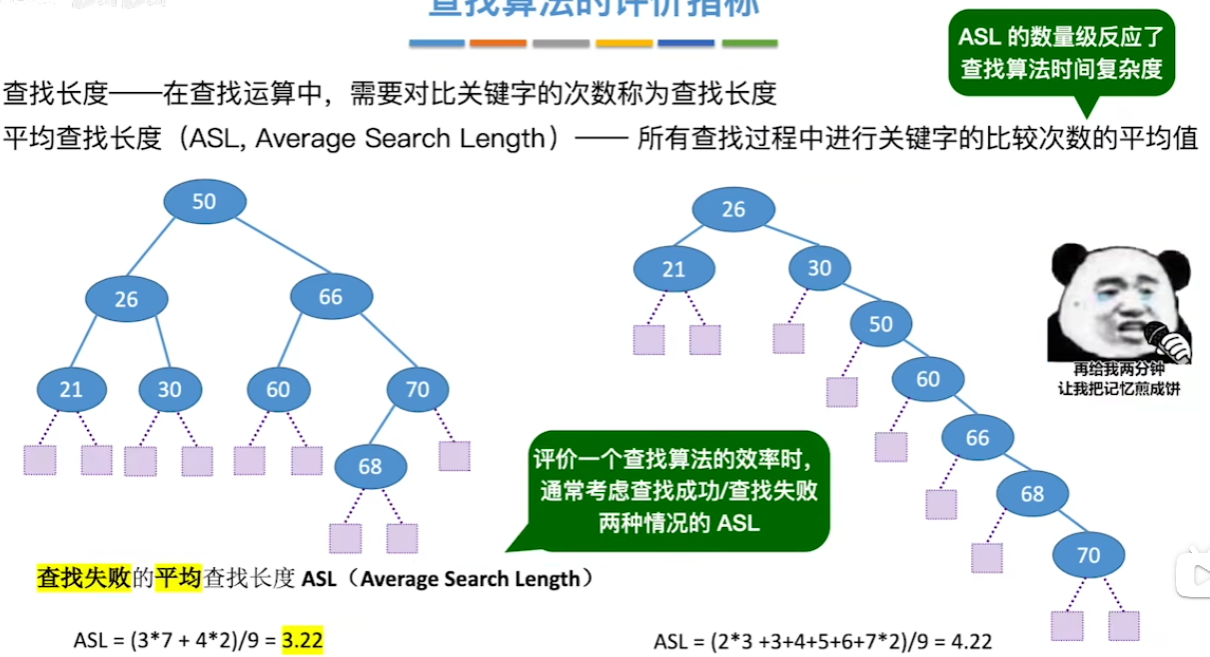
image-20241015234213068

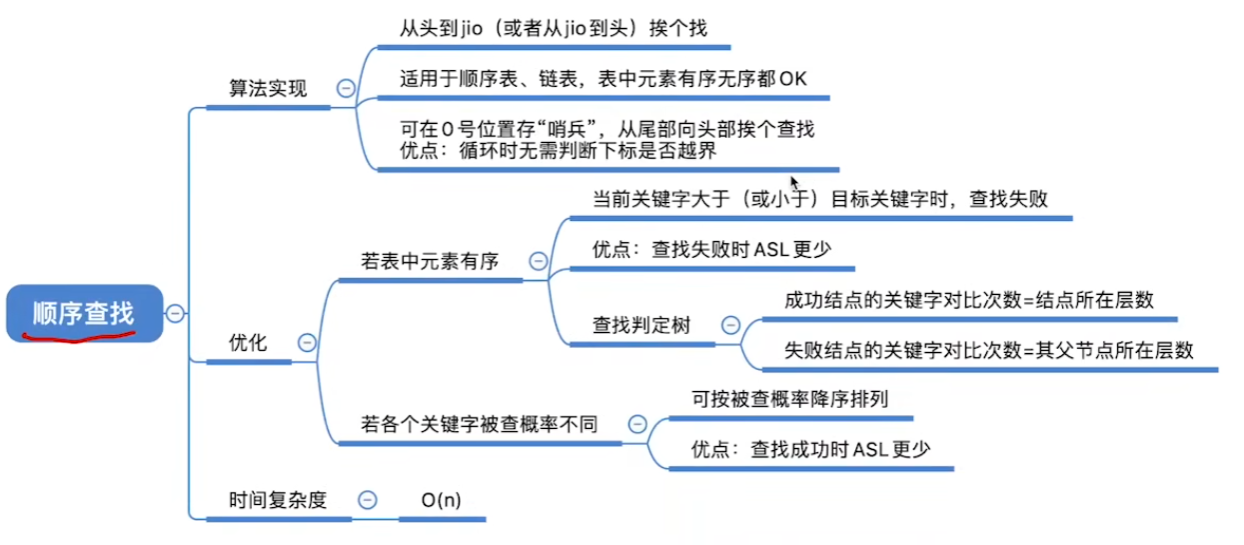
顺序查找

原理

顺序查找，又叫“线性查找”，通常用于线性表。
就是将整个数据结构进行遍历，从头到尾或者从尾到头

代码实现

image-20241015233118807

算法优化

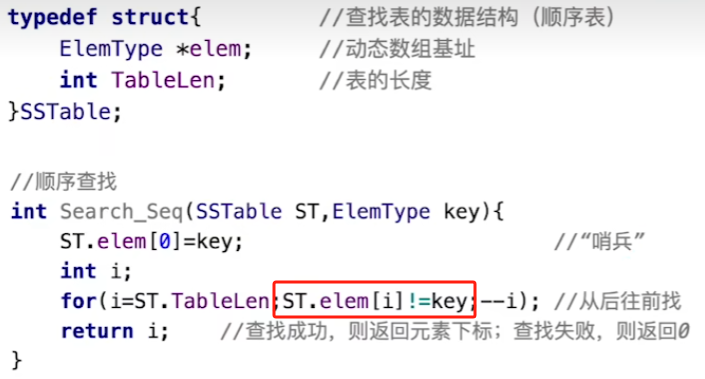
原理

设置“哨兵”元素，无需判断是否越界，执行效率更高

image-20241015233500830

代码实现

image-20241015233405791

ASL

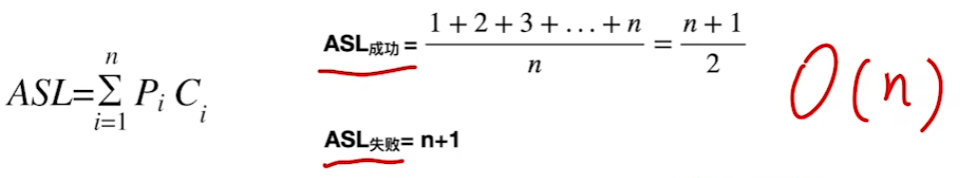
image-20241015233612606

顺序查找有序表优化

原理

对有序表进行的顺序查找

ASL

查找失败

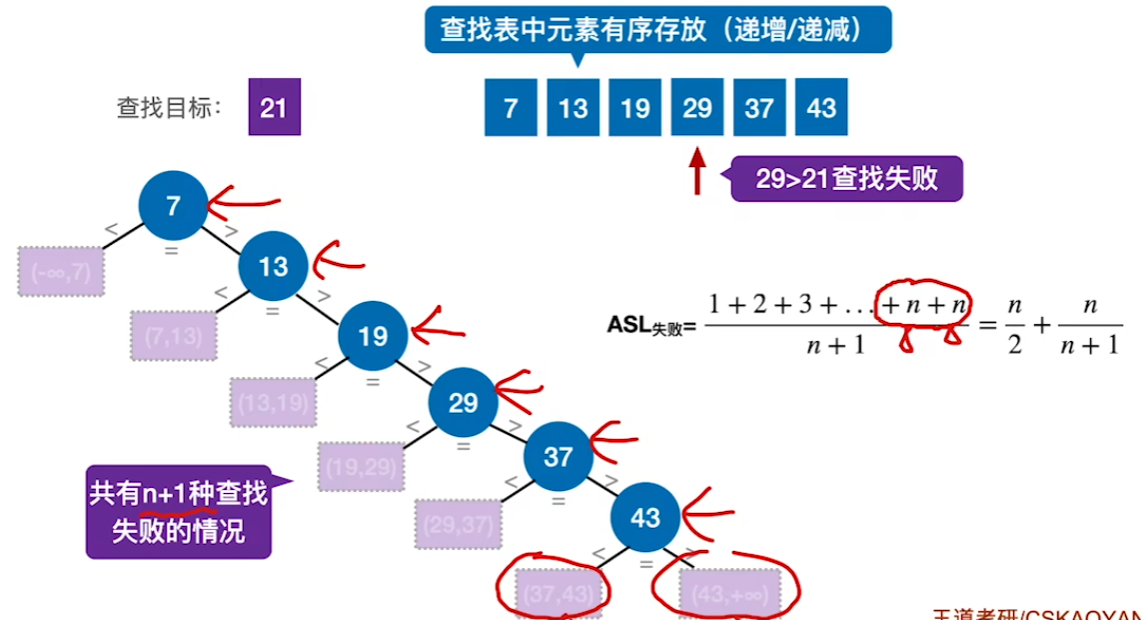
image-20241015235050753

查找成功

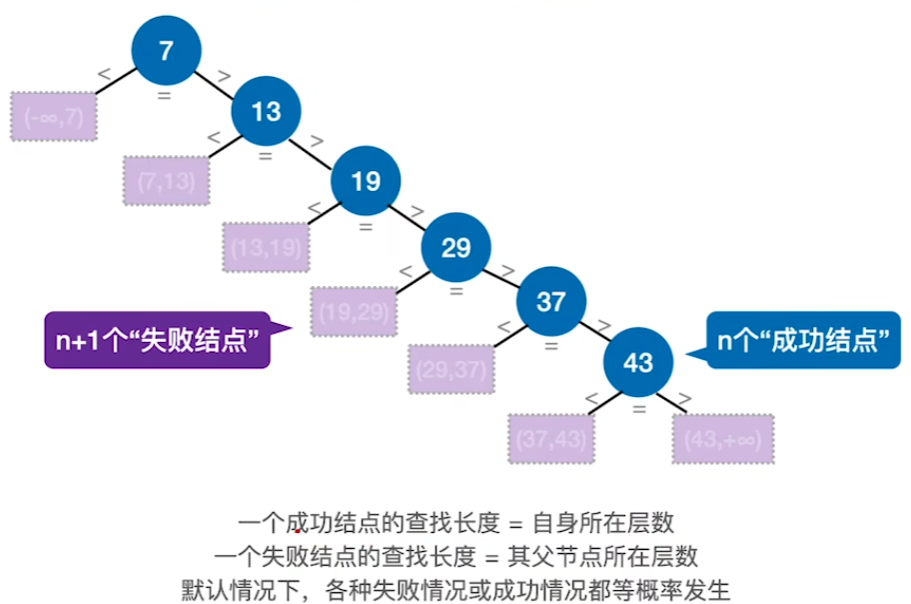
image-20241015235114678

顺序查找被查概率不相等优化

查找失败也是从头到尾全部遍历——根据实际应用查找的情况来考虑

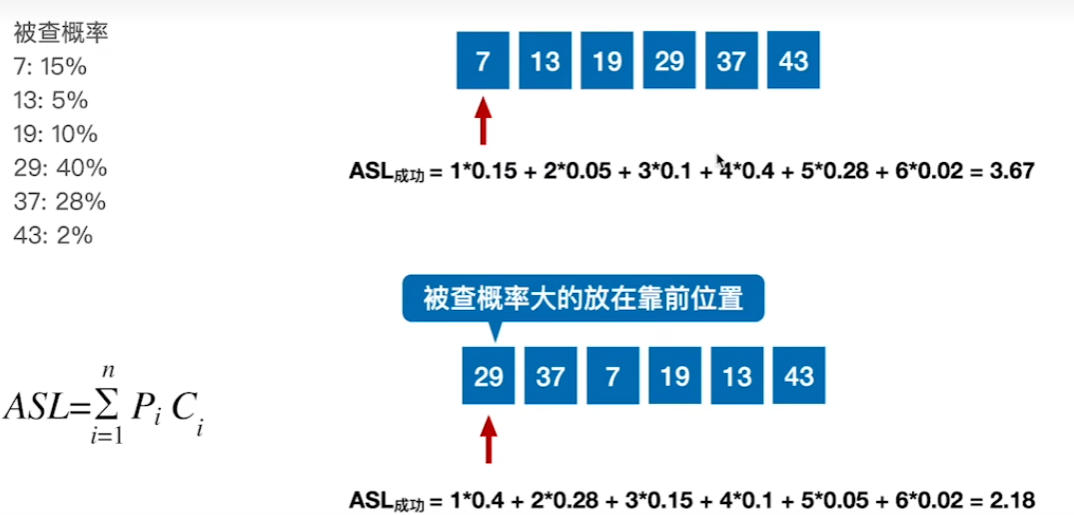
image-20241015235547535

总结

image-20241015235731665

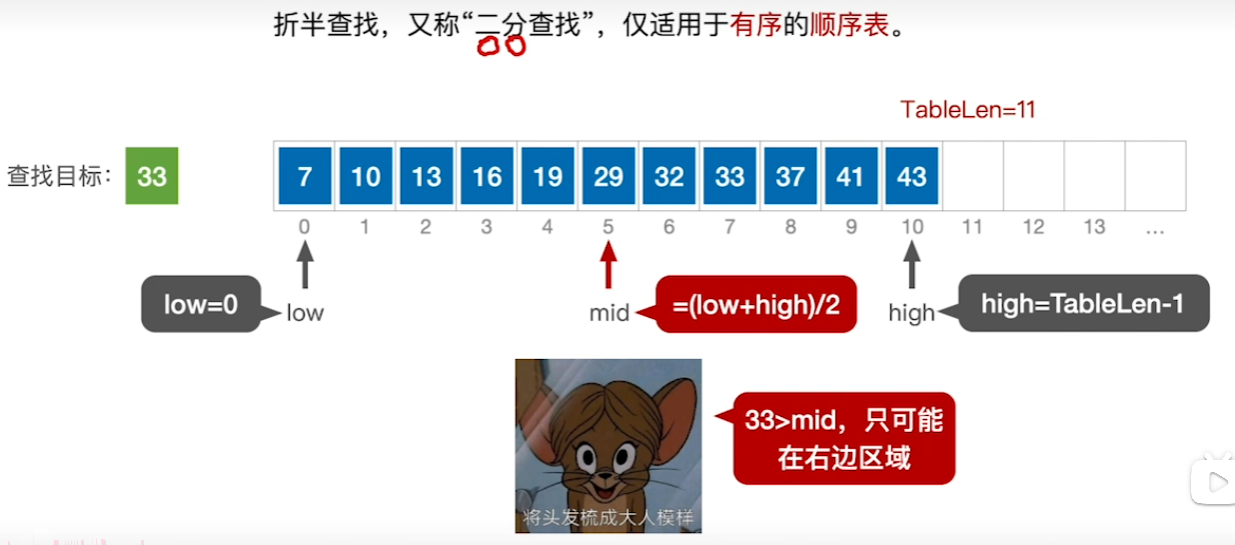
折半查找（二分查找）

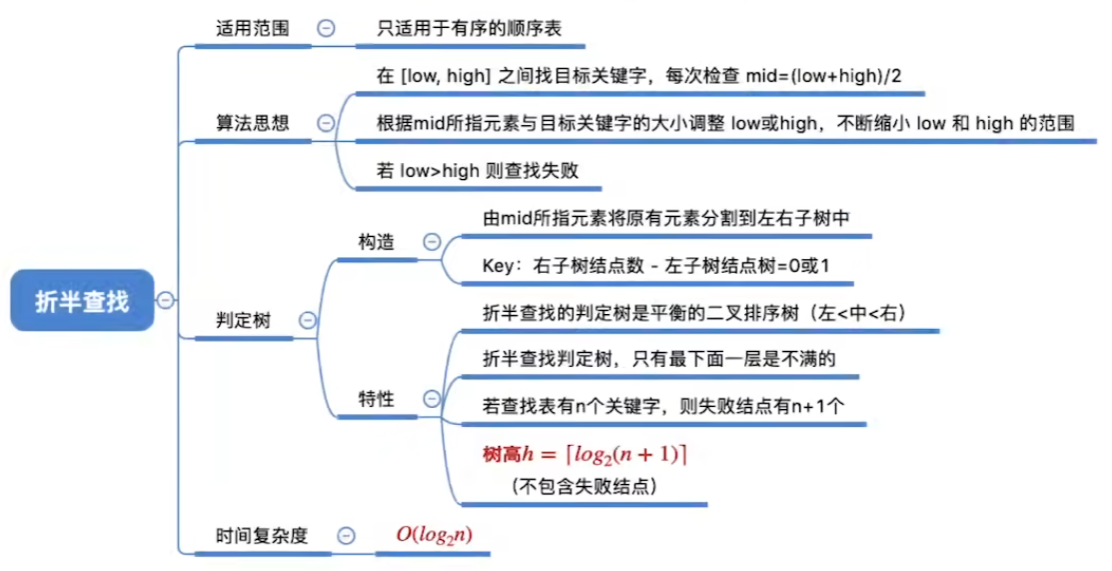
原理

对半砍来查找，但只适用于有顺序的，不然无法进行二分查找

简单来说就是数字炸弹

例：找78->0~100(50)->50~100(75)->75~100(87)->75~87(81)->75->81(78)->78

image-20241016000343108

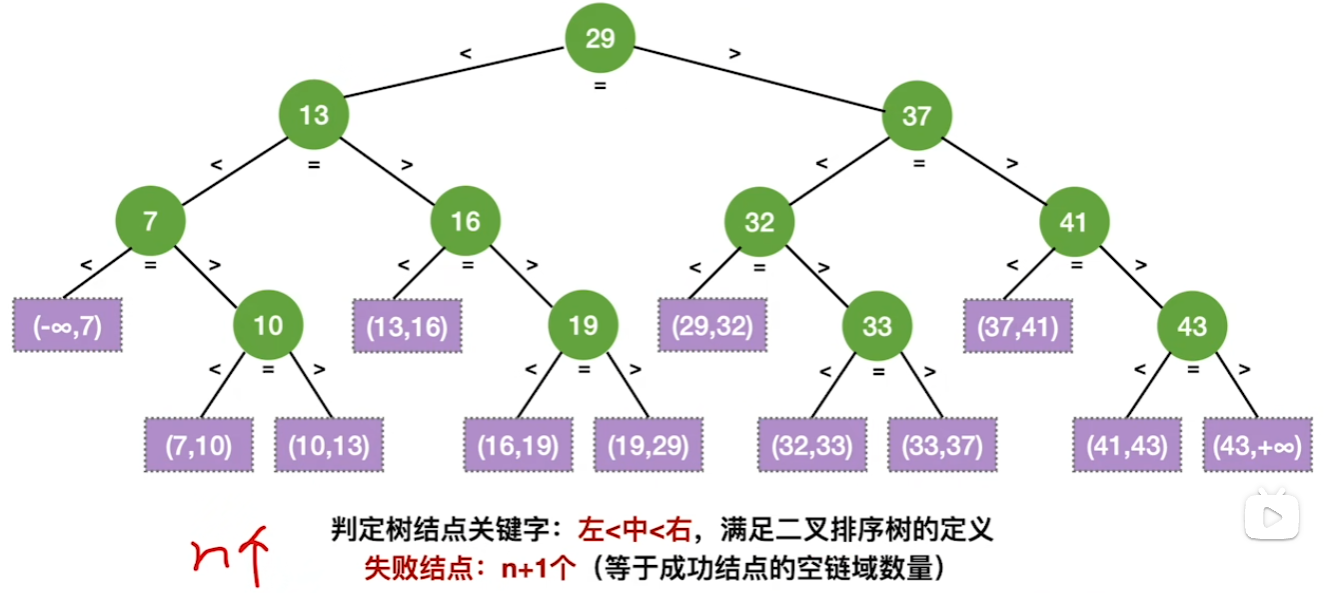
折半查找判定树

性质

image-20241016001133712

失败结点

image-20241016001221740

ASL

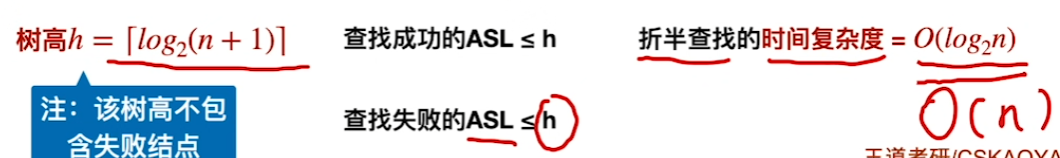
image-20241016001323297

代码实现

image-20241016000736311

ASL

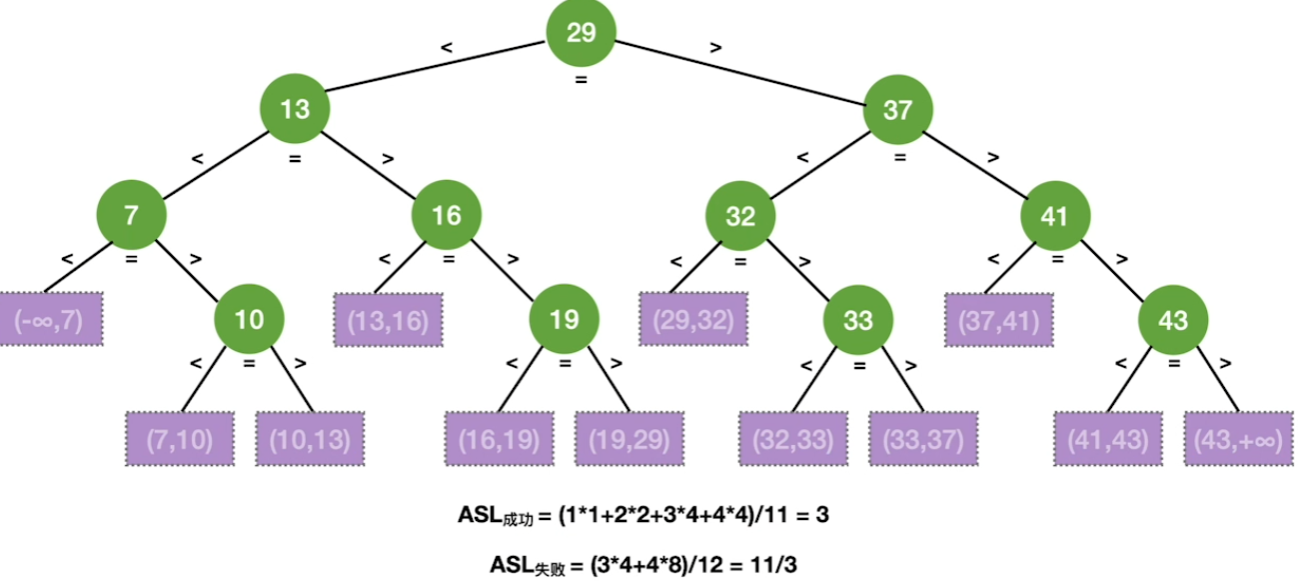
image-20241016000828138

总结

image-20241016001347343

分块查找

原理

将需要查找的原始表进行分块，构造索引表

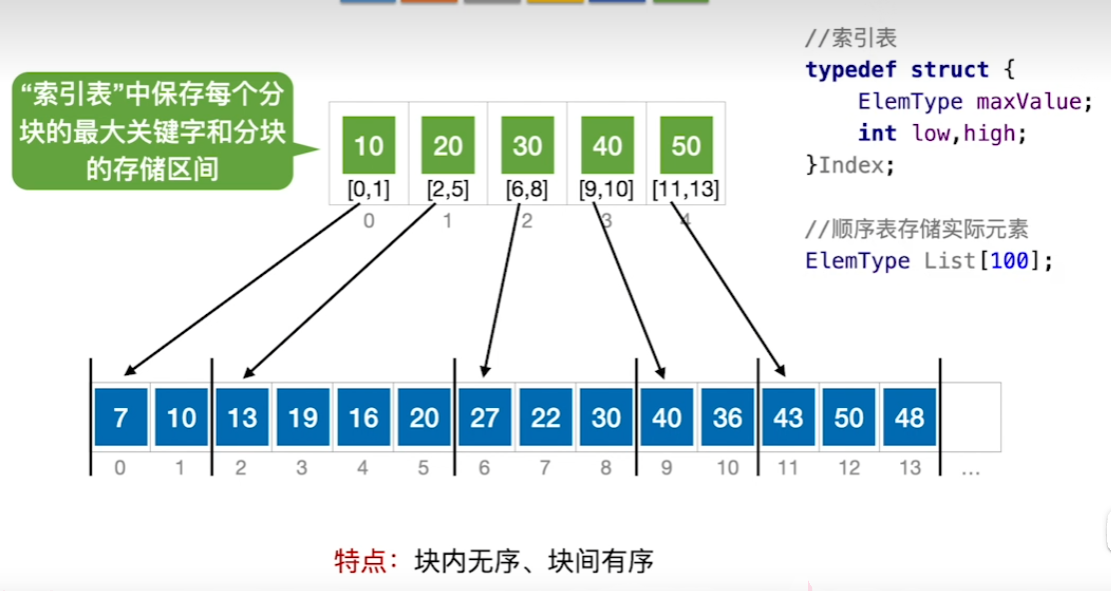
image-20241016001902659

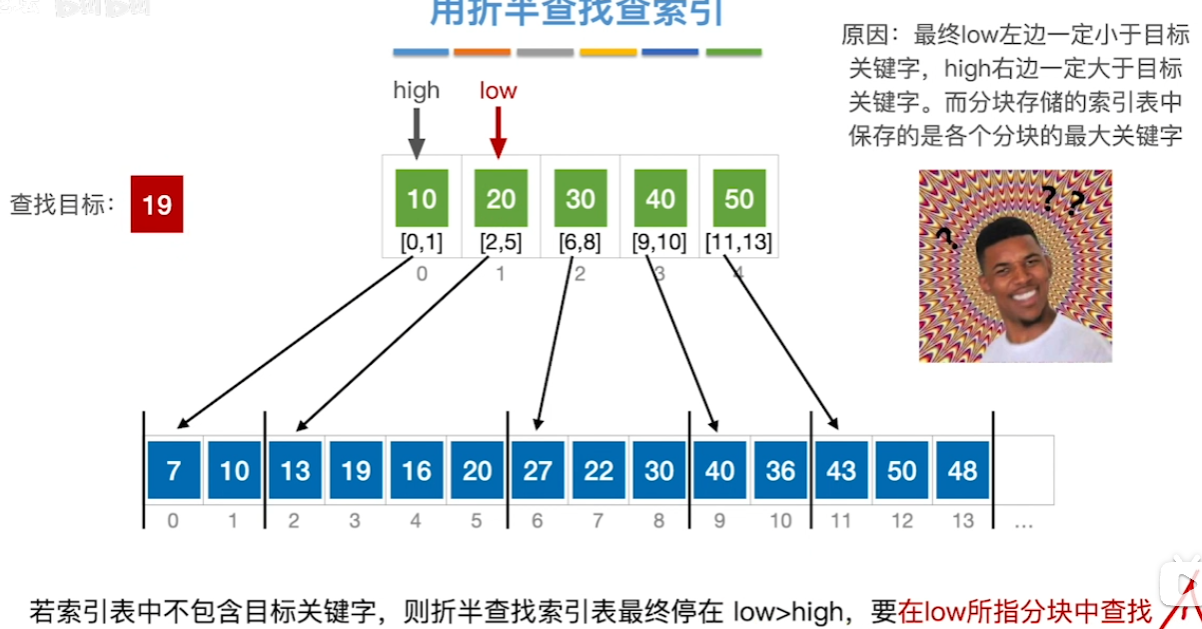
image-20241016002645953

ASL

已知情况

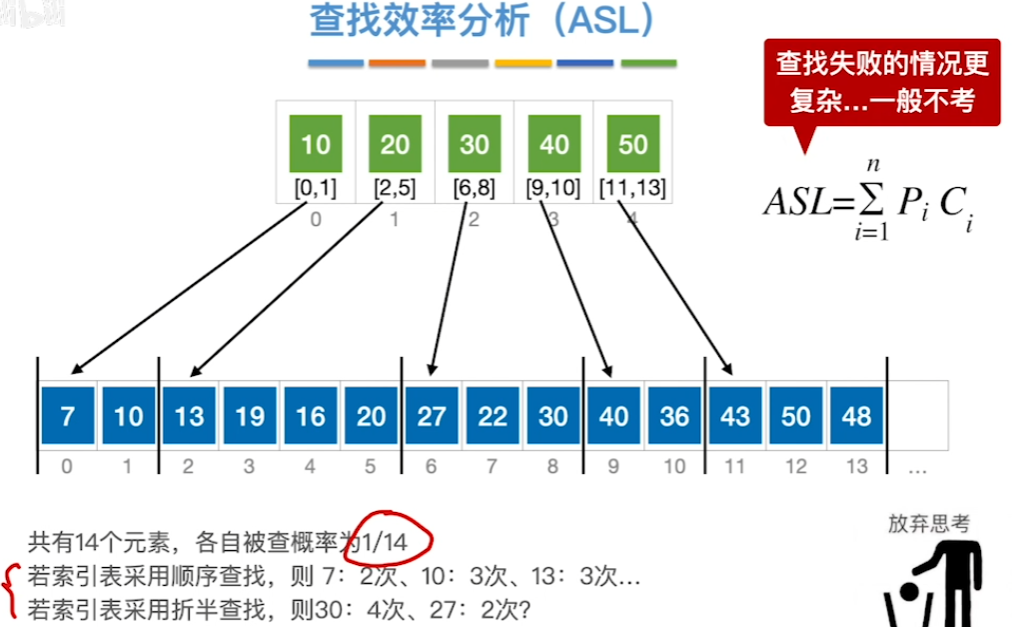
image-20241016003320841

未知情况

顺序查找常考

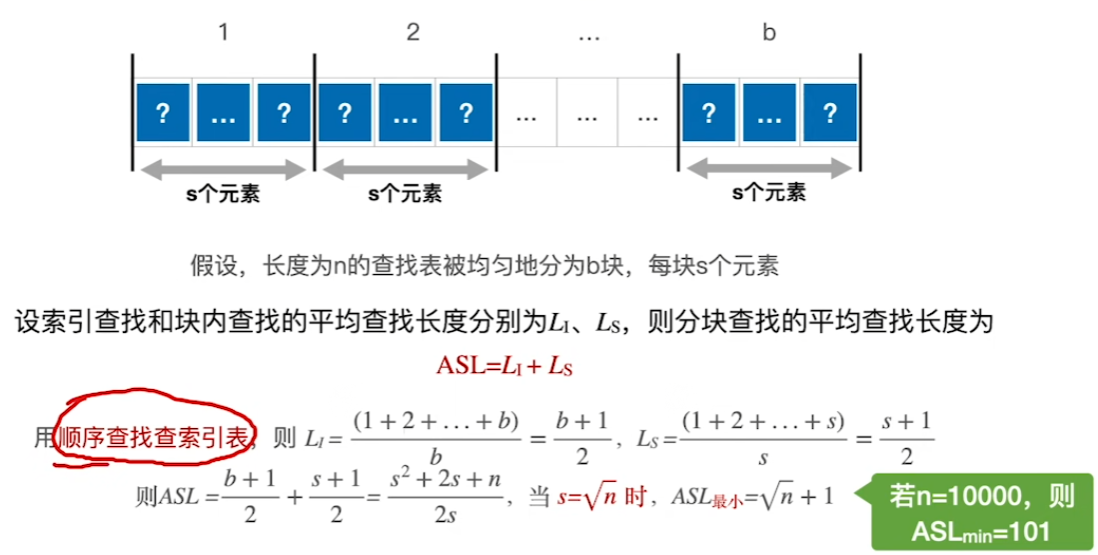
image-20241016003359815

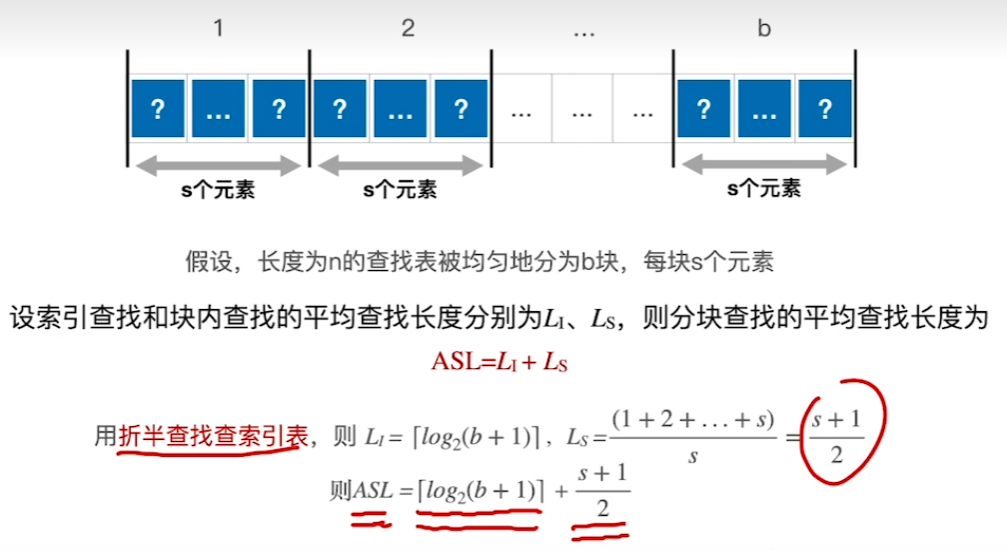
image-20241016003410658

总结

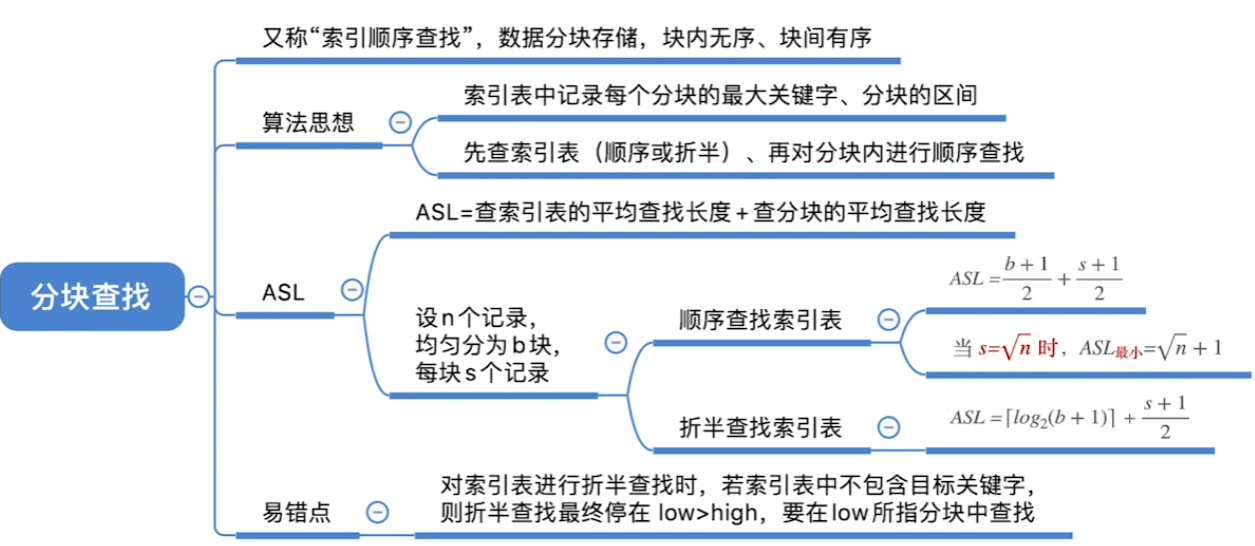
image-20241016003511188

BST（二叉排序树）

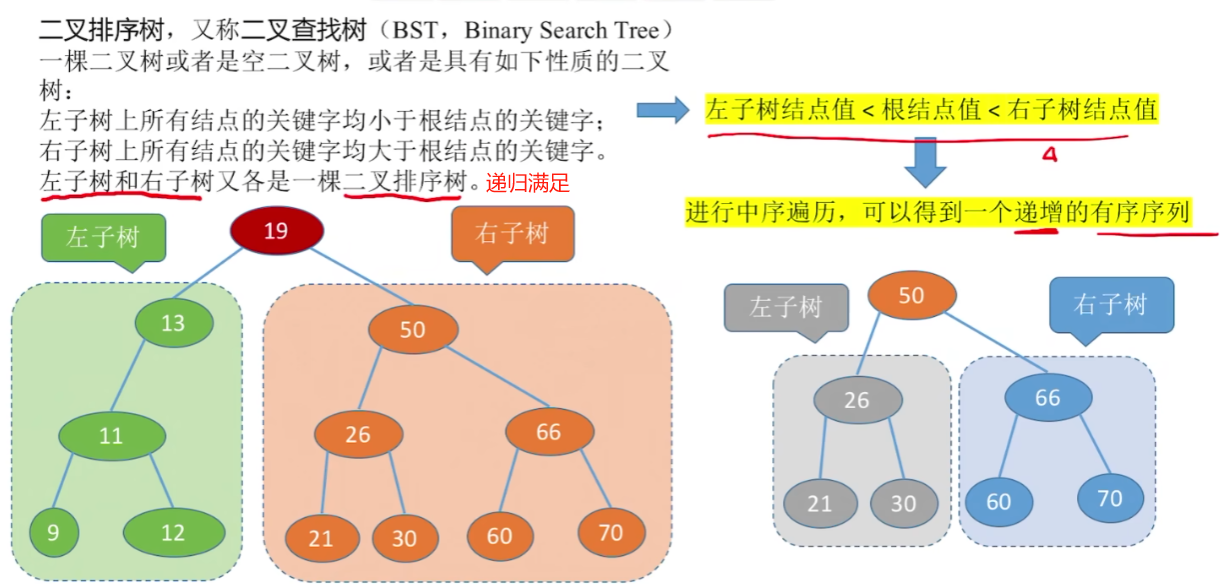
概念

一个二叉树满足左子树结点数值<根结点数值<右子树结点数值

image-20241016003829552

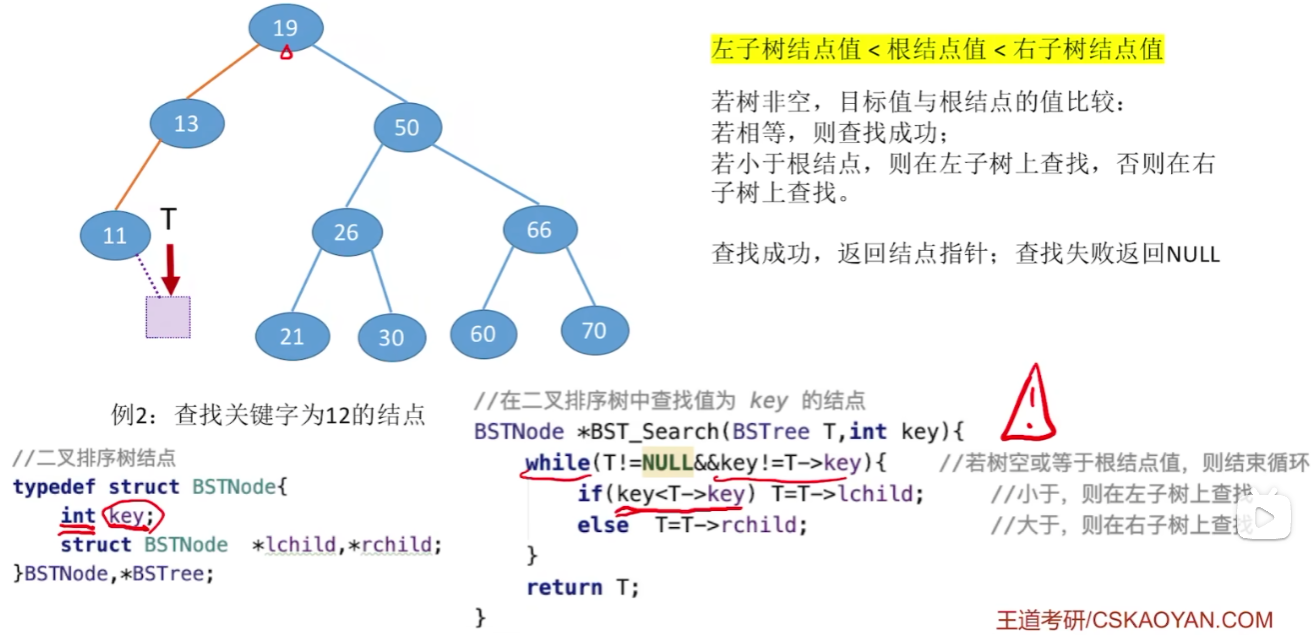
查找操作

非递归代码实现

image-20241016004213562

递归代码实现

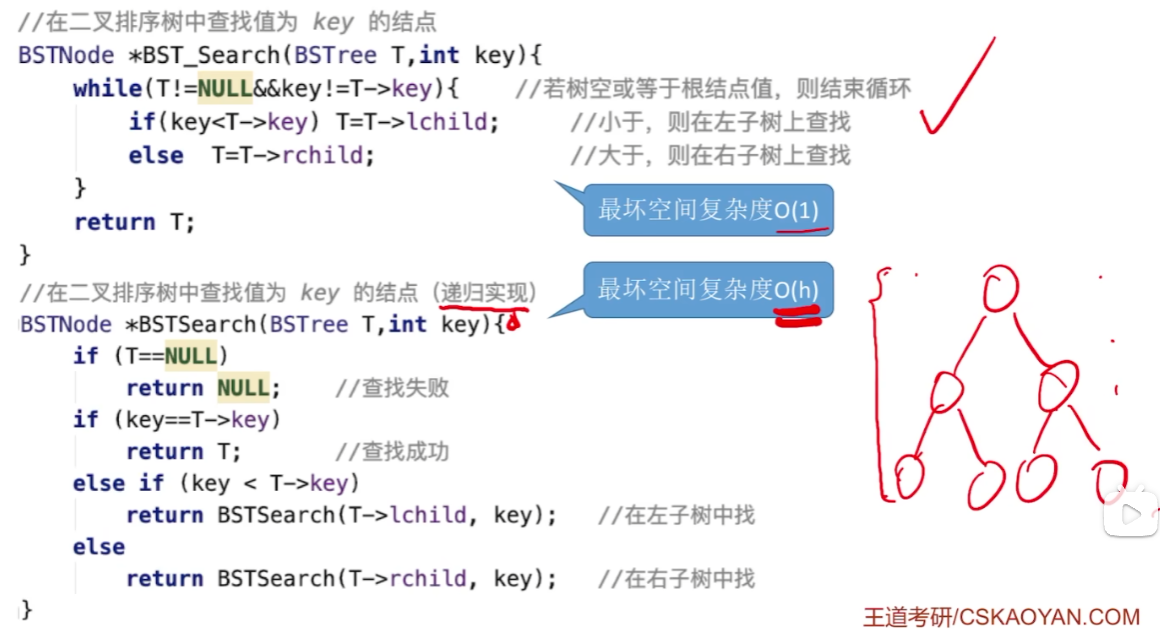
image-20241016004335732

比较

由于递归调用函数会在函数调用栈里面多分配空间，会浪费更多空间，所以一般使用非递归调用

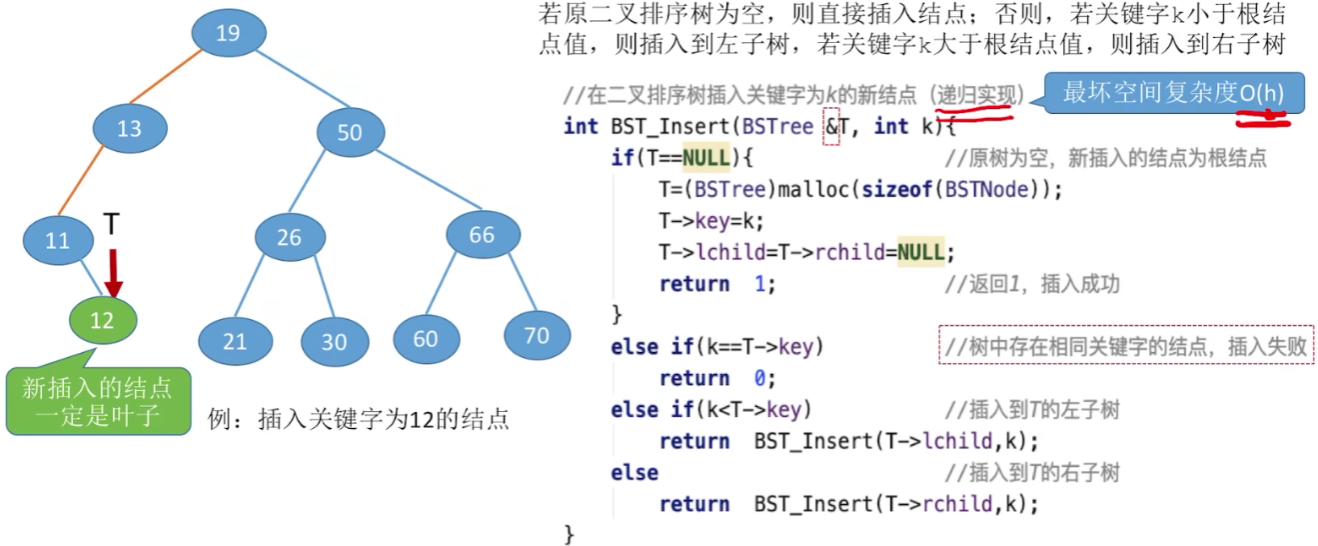
插入操作

插入后的新结点一定是叶子结点

image-20241016004701665

删除操作

删除结点为叶子结点

直接删除，不会破坏二叉排序树的性质

删除结点只有一棵左子树或者右子树

让z的子树成为z父结点的子树，替代z的位置

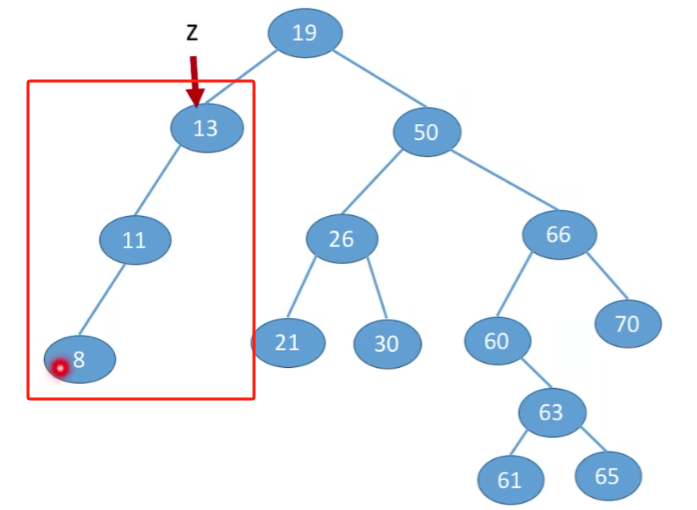
image-20241016005357333

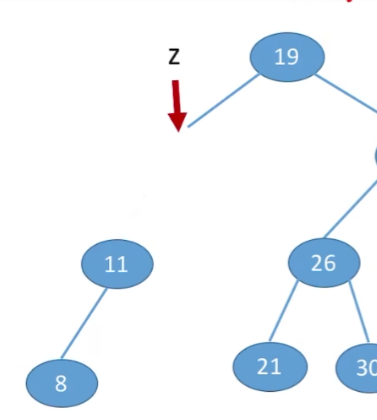
image-20241016005406555

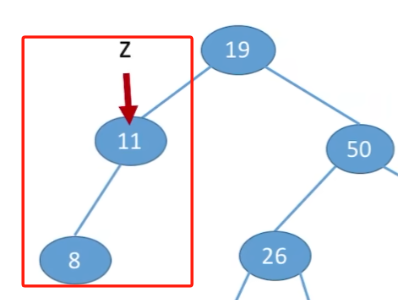
image-20241016005420708

删除结点有左右子树

若结点z有左、右两棵子树，则令z的直接后继(或直接前驱)替代z然后从二叉排序树中删去这个直接后继(或直接前驱)，这样就转换成了第一或第二种情况

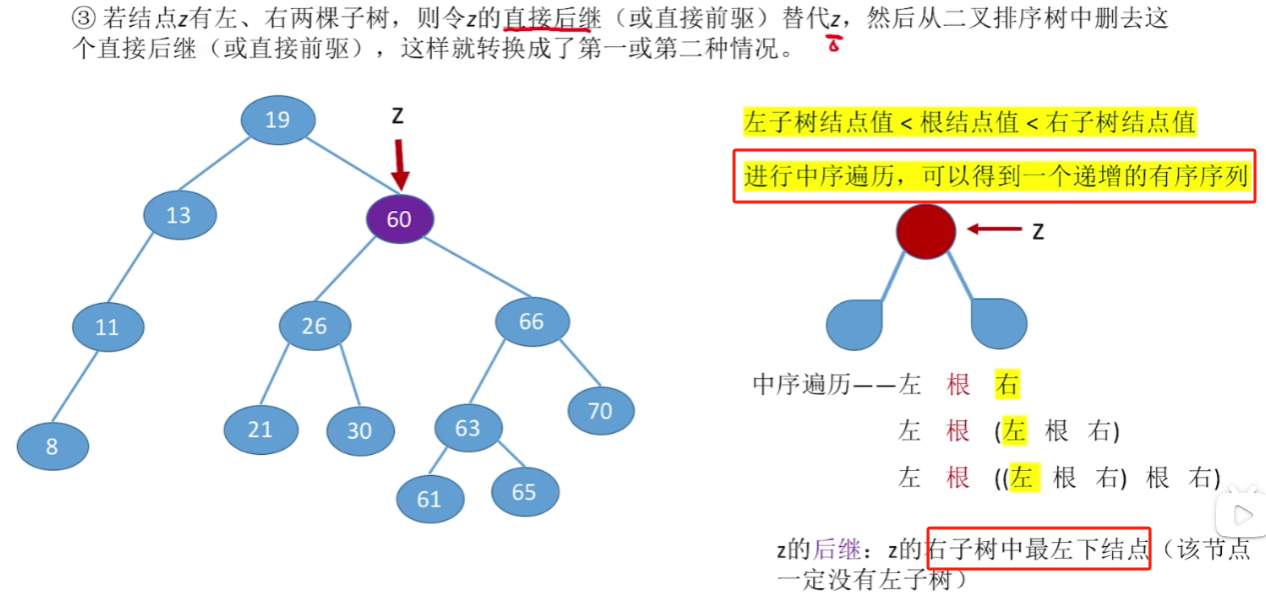
image-20241016011204188

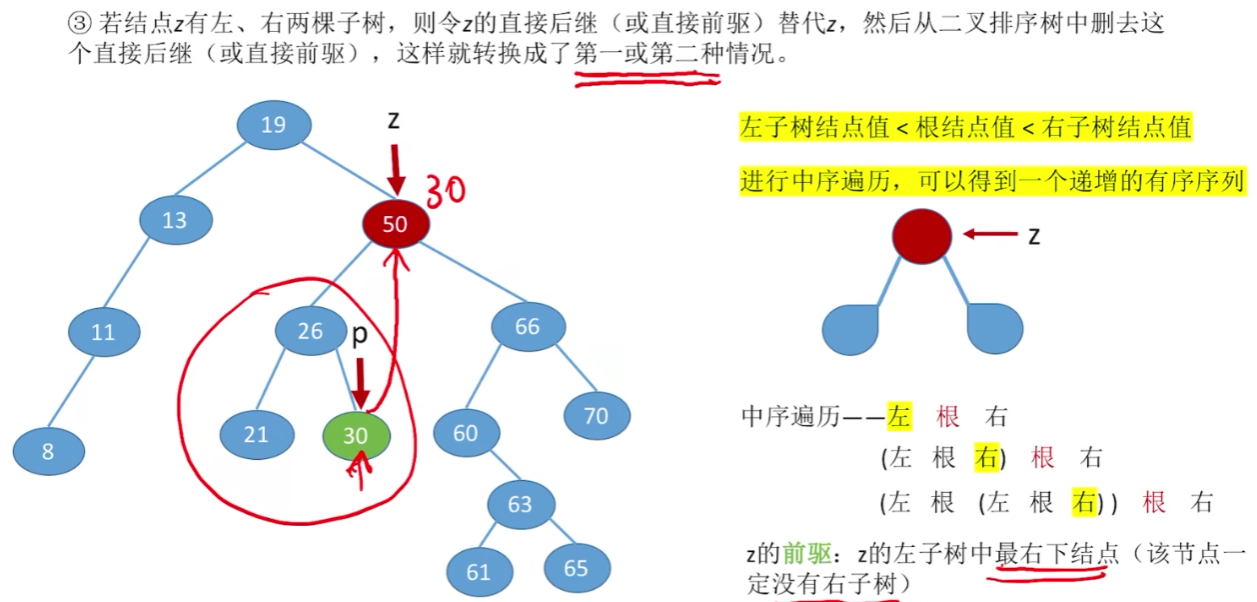
image-20241016011348911

ASL

查找成功

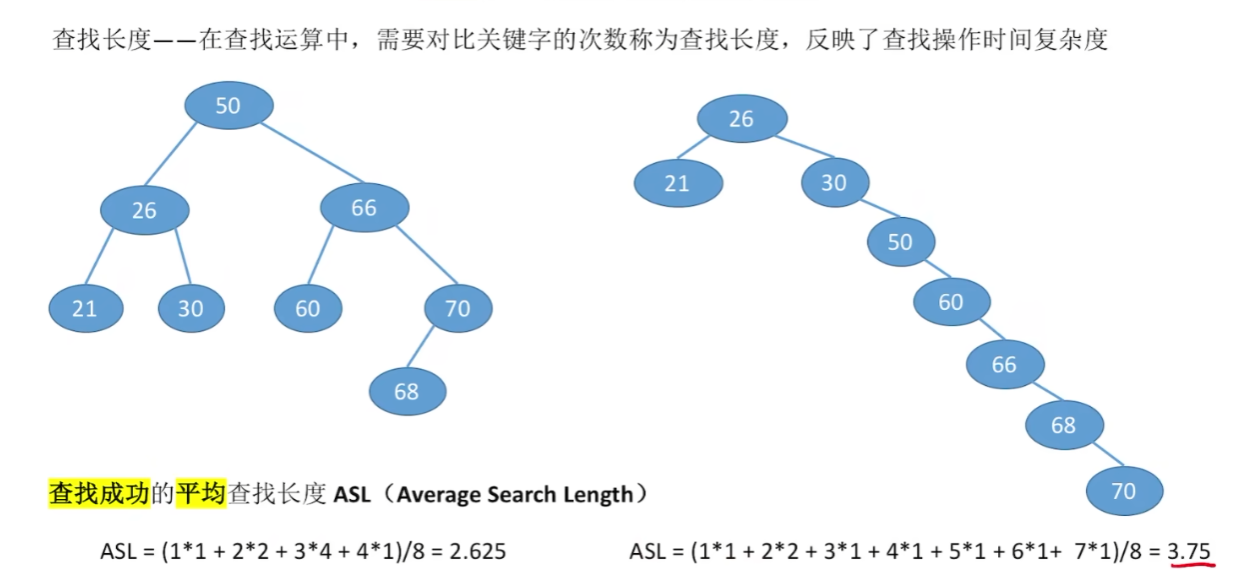
image-20241016011515718

image-20241016011608949

查找失败

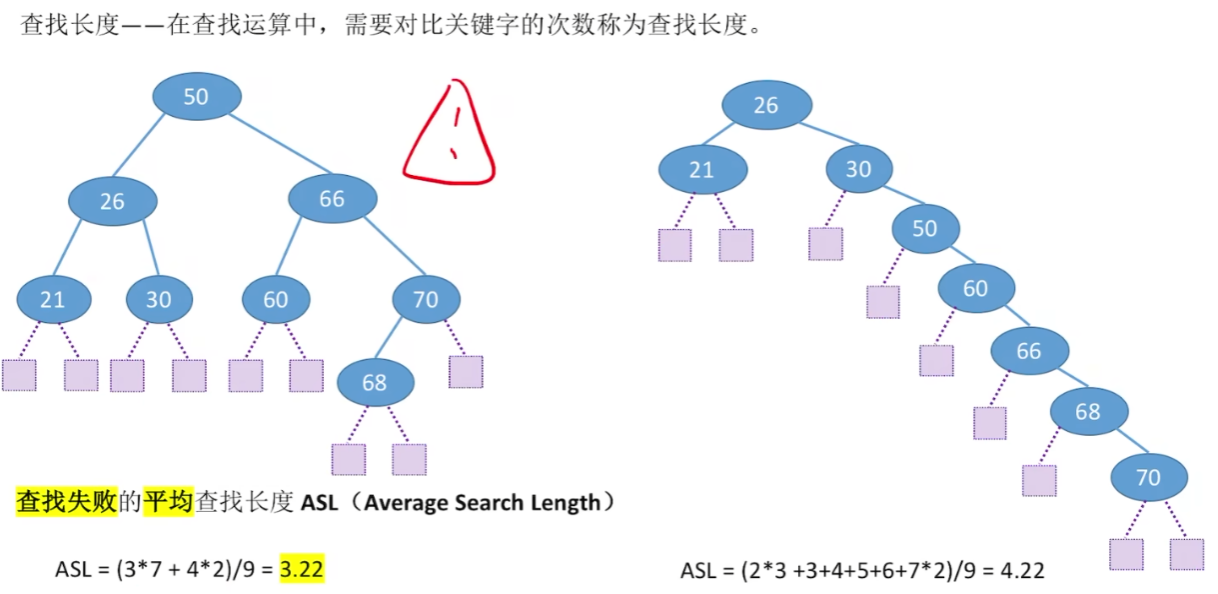
image-20241016011728126

总结

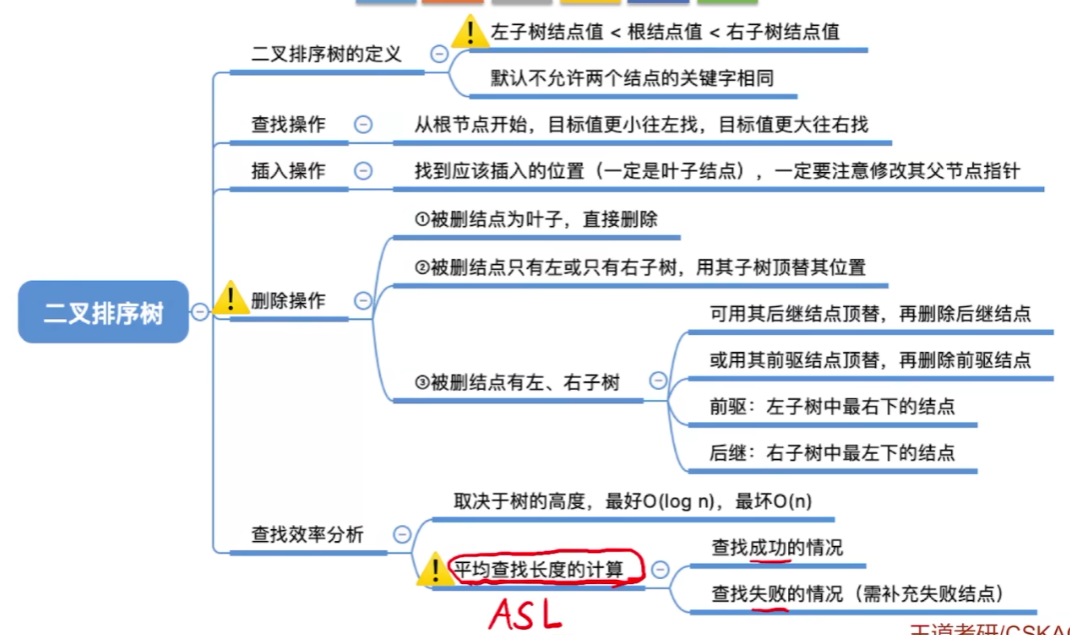
image-20241016011749147

AVL（平衡二叉树）

定义

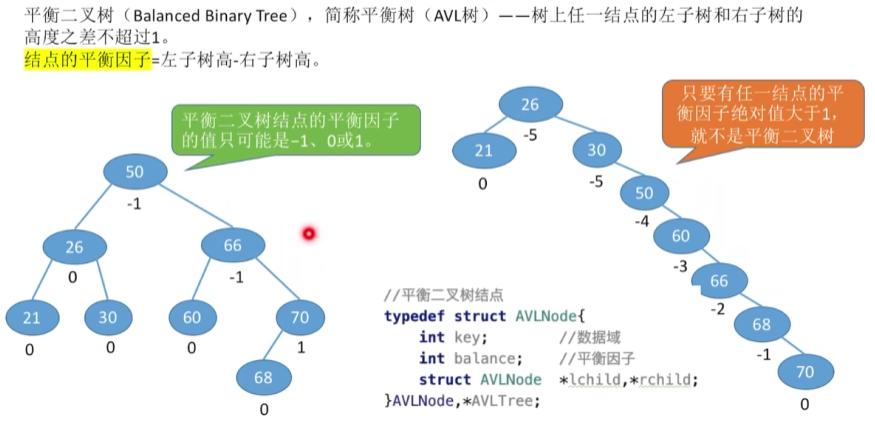
image-20241016141027788

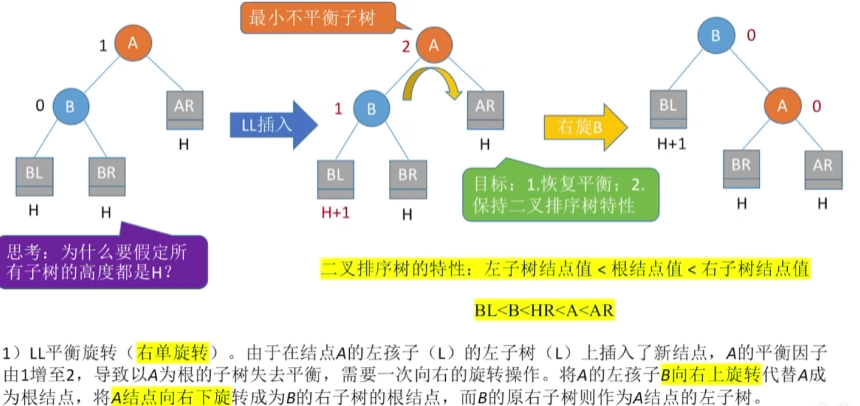
调整最小不平衡二叉树

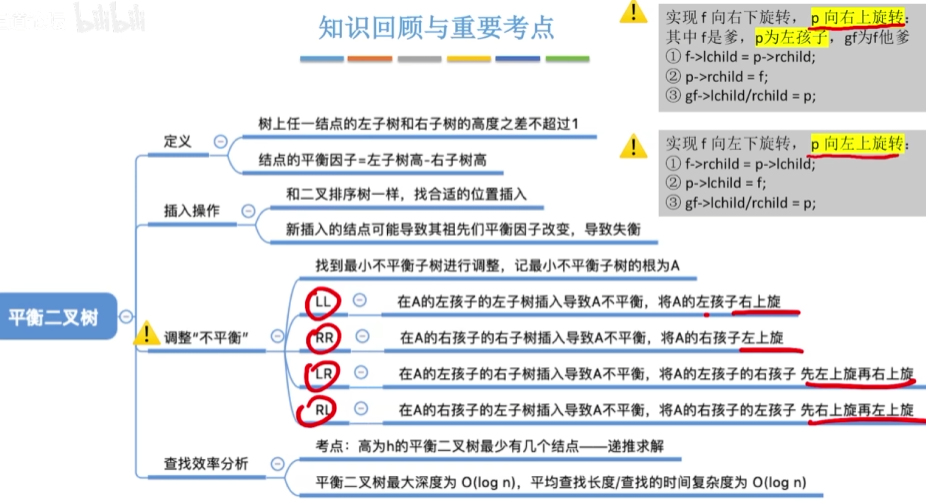
LL（左孩子右上旋）

image-20241016141206656

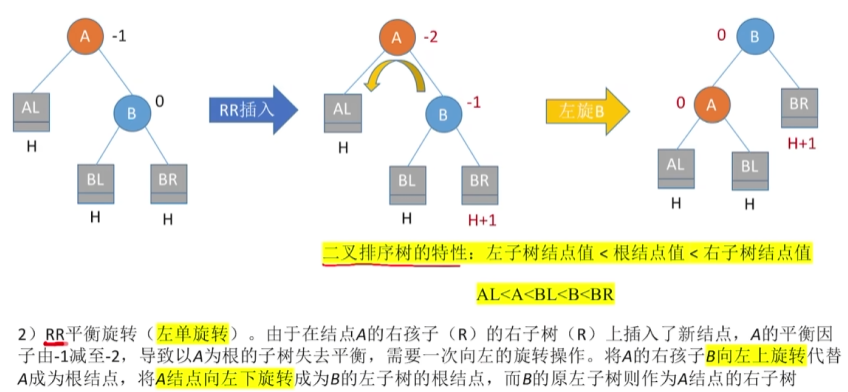
RR（右孩子左上旋）

image-20241016141238767

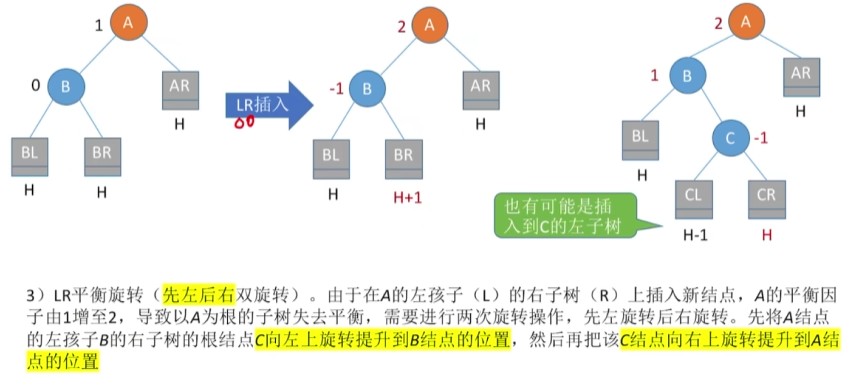
LR（左孩子的右孩子先左上旋再右上旋）

image-20241016141359300

RL（右孩子的左孩子先右上旋再左上旋）

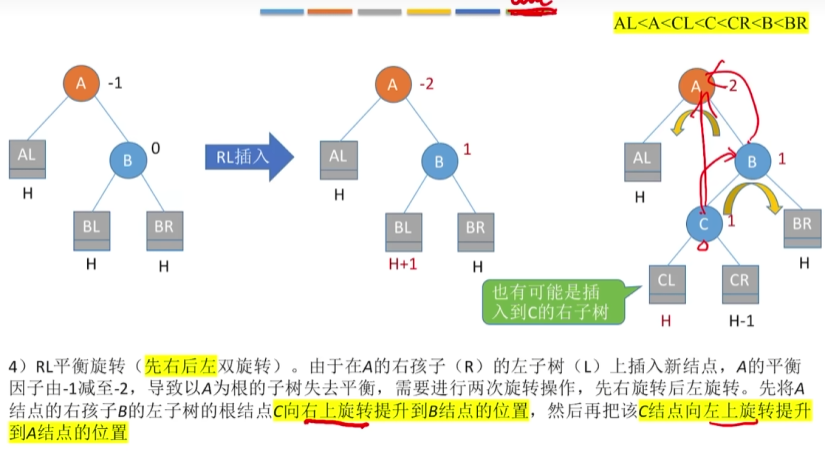
image-20241016141440006

代码实现

LL与RR

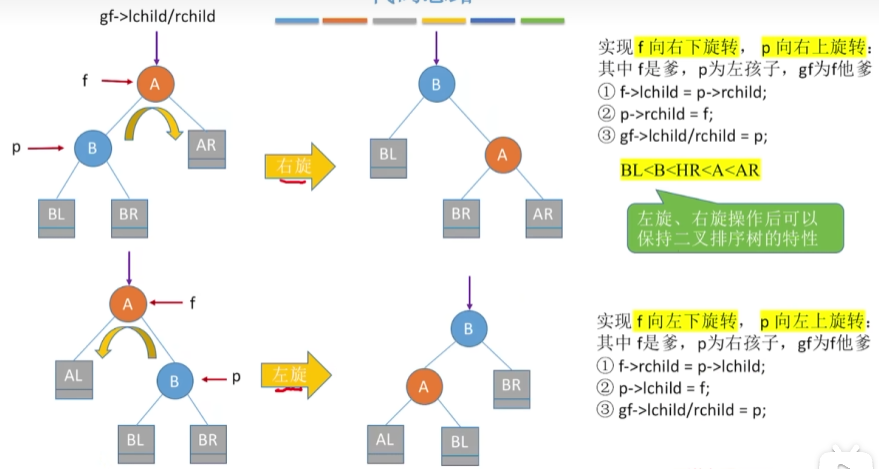
image-20241016141307309

总结

image-20241016141828444

平衡二叉树的删除

image-20241016142630111

image-20241016142751853

ASL

image-20241016141805536

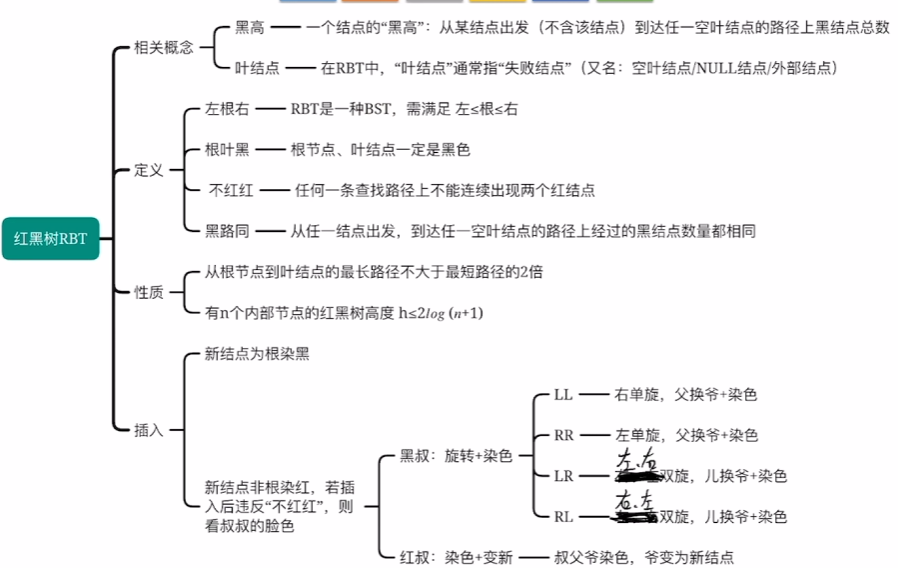
RBT（红黑树）

区别

红黑树更适合需要频繁进行修改的场景

image-20241016143209908

定义

image-20241016143259508

性质

image-20241016143335964

时间复杂度

image-20241016143354271

插入操作

image-20241016143432781

提示

染色对应前面的具体结点

比如父换爷＋染色——对应就是原本的父节点和爷结点进行染色

变新意思为将该叔结点经过染色后再当做是新插入的结点再将其以插入操作从上到下进行操作

总结

image-20241016143850696

B树

定义

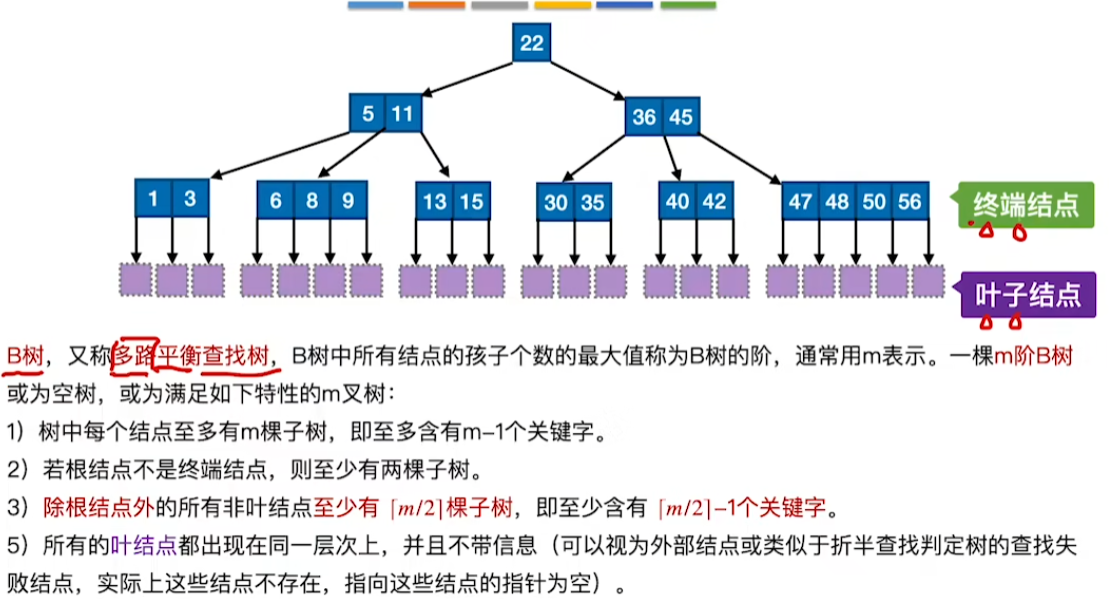
image-20241016232030976

特征性质

image-20241016234113590

高度范围

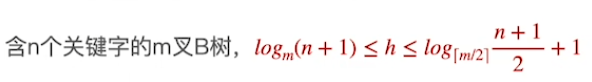
image-20241016234133167

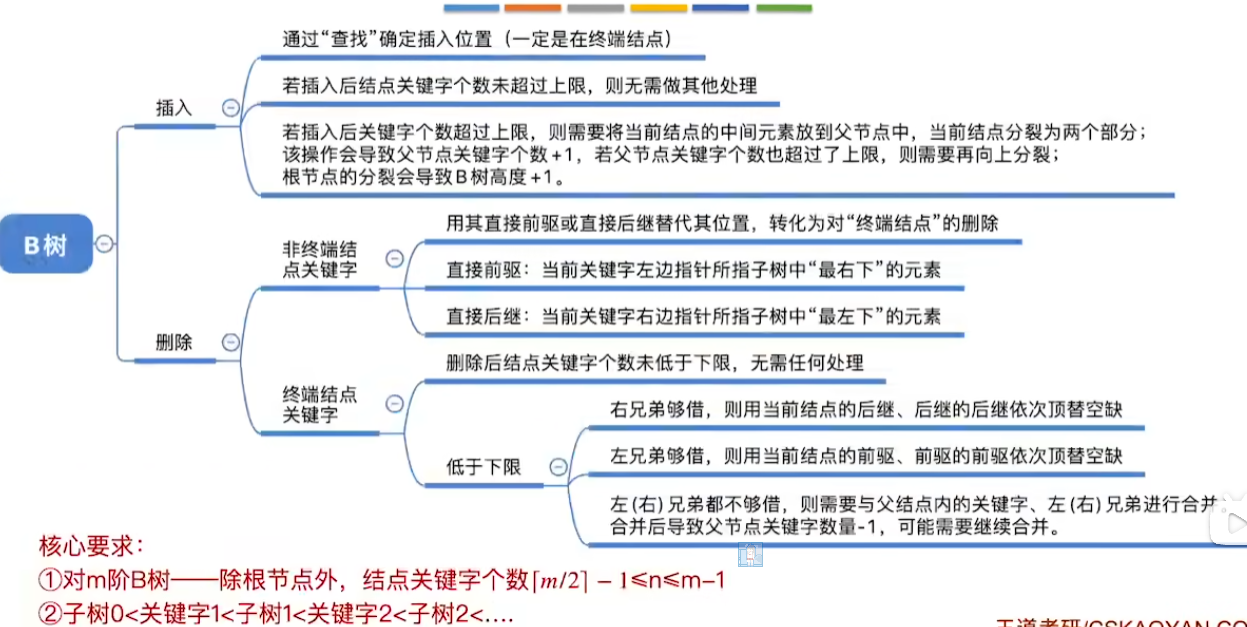
插入操作

前提要求

image-20241017000028731

过程

1、通过B树的查找，确定插入的位置，只能是终端节点

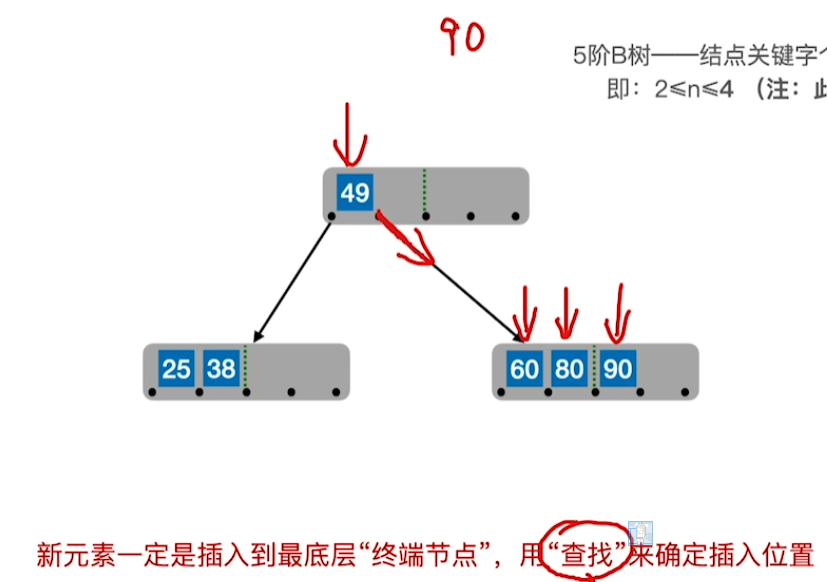
image-20241017000116578

2、若关键字个数超出范围，则将中间位置（[m/2]向上取整）向上提，其后面的关键字放到新的结点中去

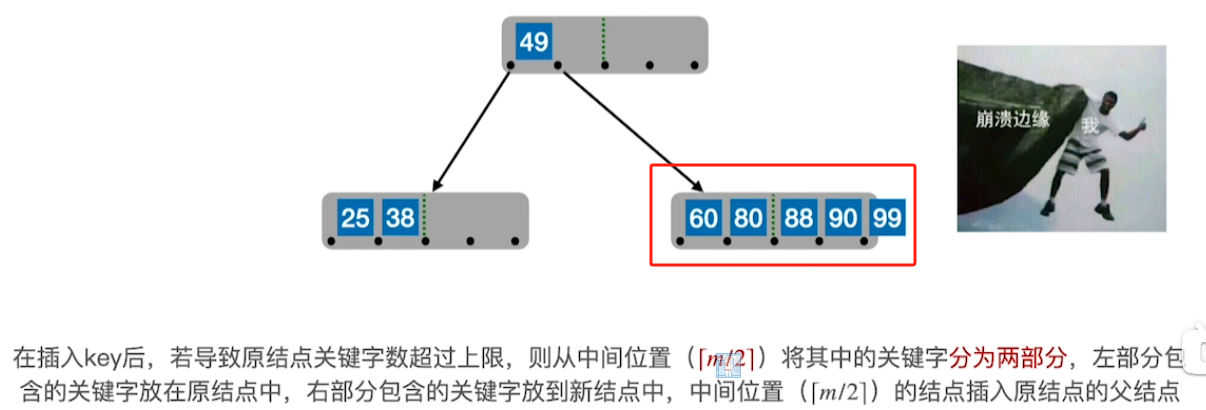
image-20241017000320572

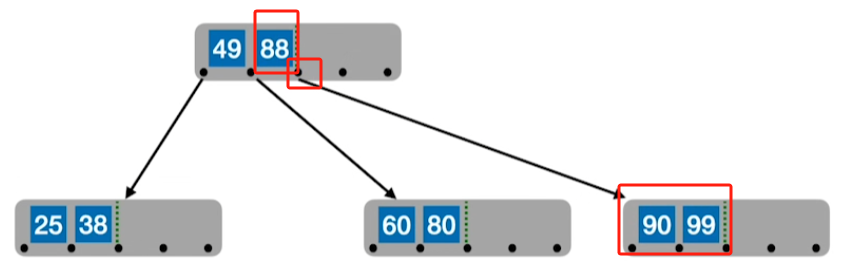
image-20241017000348610

3、若父节点的关键字个数超了，也同上一样提中间数其后关键字放新结点

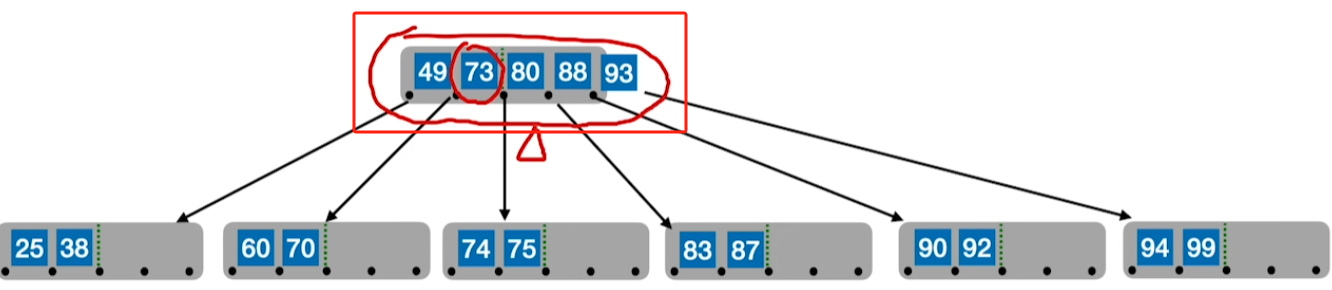
image-20241017000519250

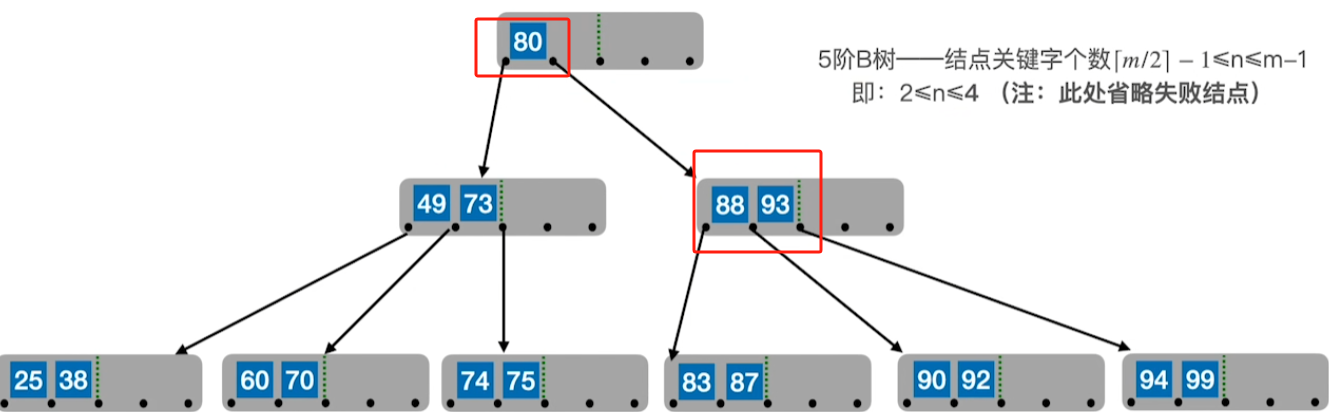
image-20241017000543103

小总结

image-20241017000615260

删除操作

过程

1、若被删除关键字在终端节点，则直接删除（注意：不能低于B数要求下限）

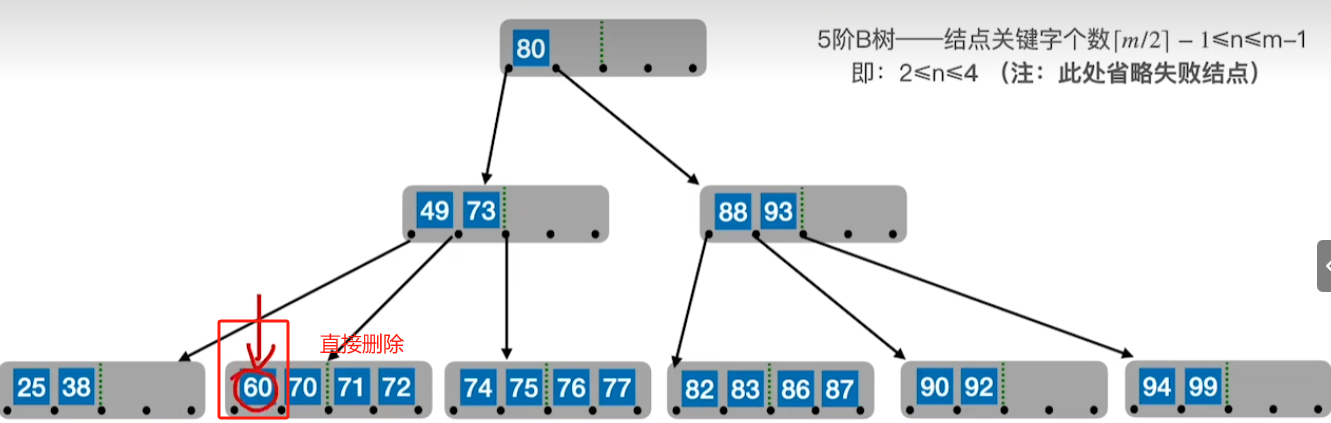
image-20241017000743507

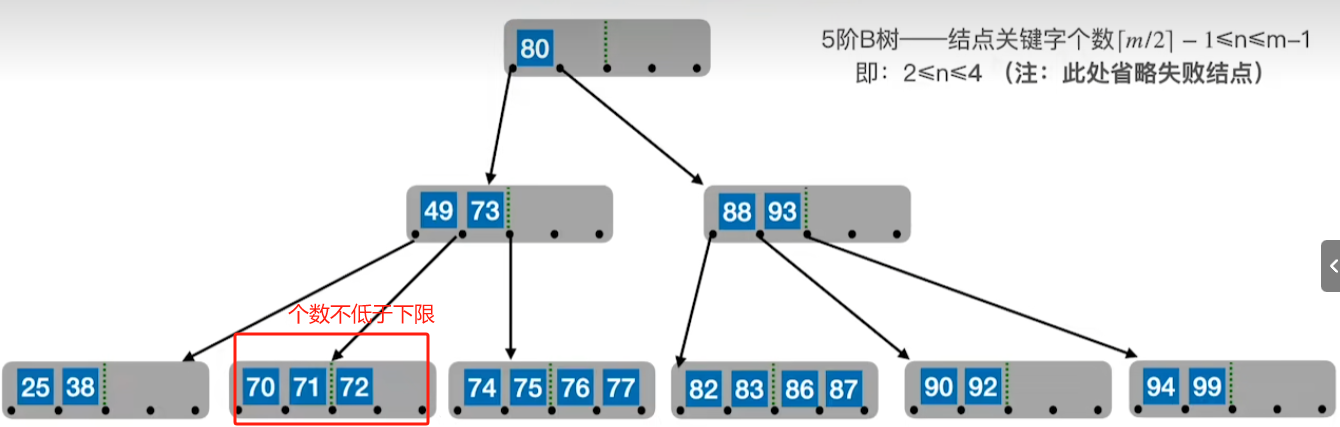
image-20241017000805432

2、若被删除关键字在非终端节点，则用其前驱或者后继来替代其位置

image-20241017000933364

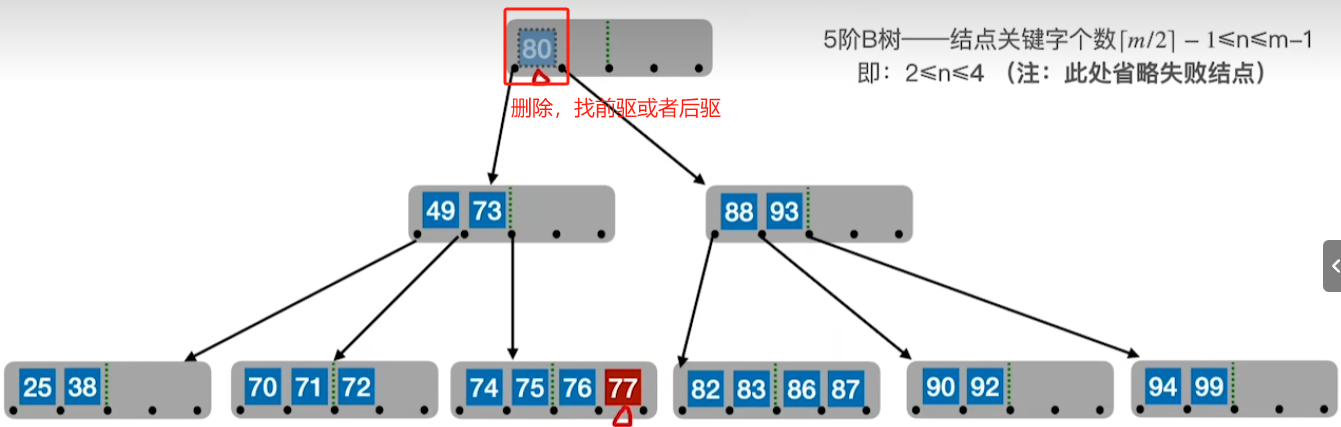
image-20241017000924229

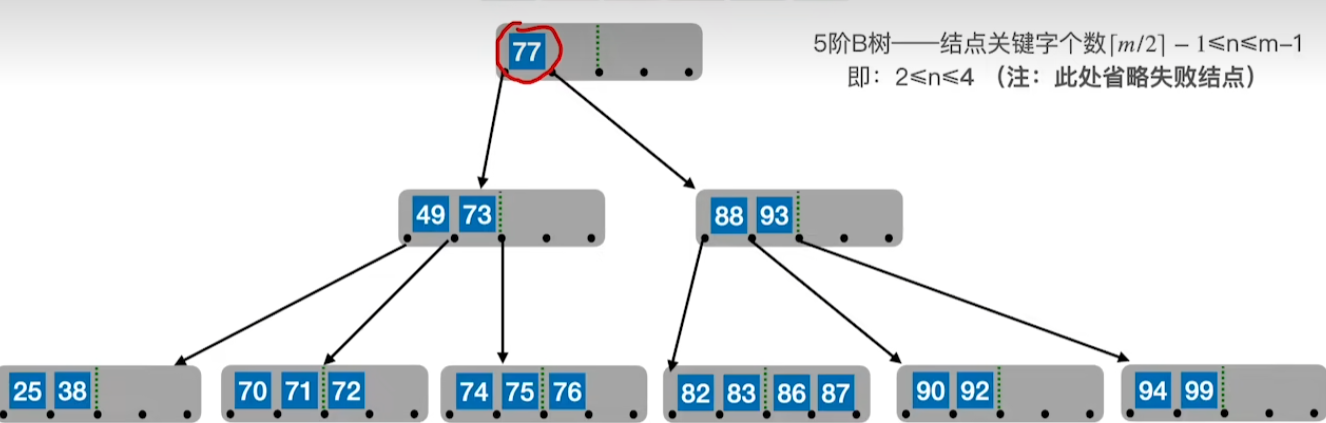
image-20241017000959176

后继

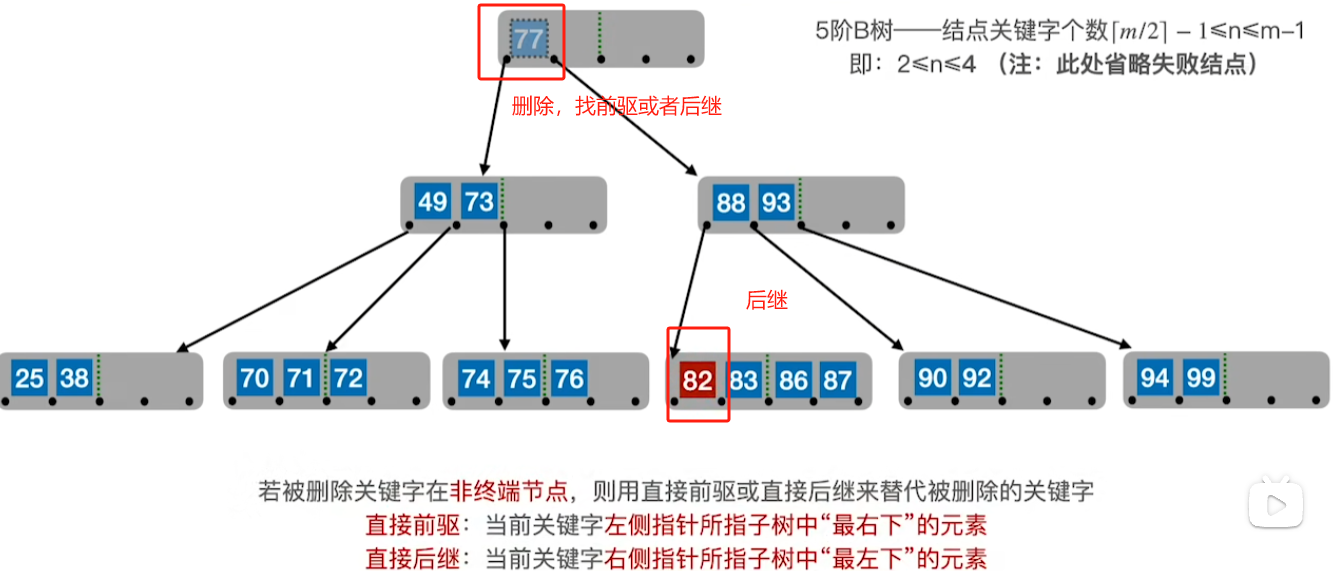
image-20241017001035943

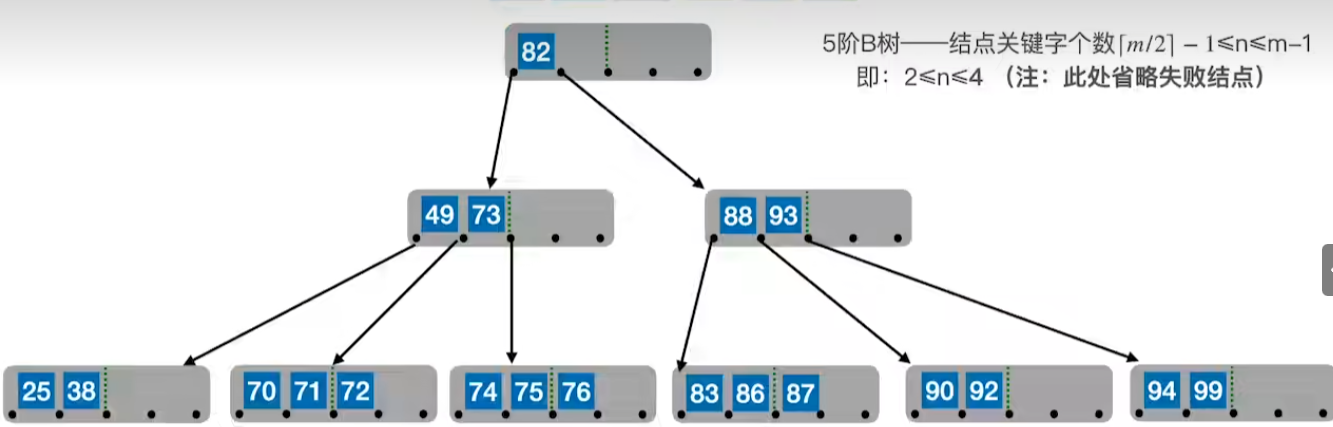
image-20241017001101355

3、若被删除关键字在终端节点，且此时低于B树下限，则拉父提兄（将父节点拉下来，兄弟节点提上去）

拉右兄弟

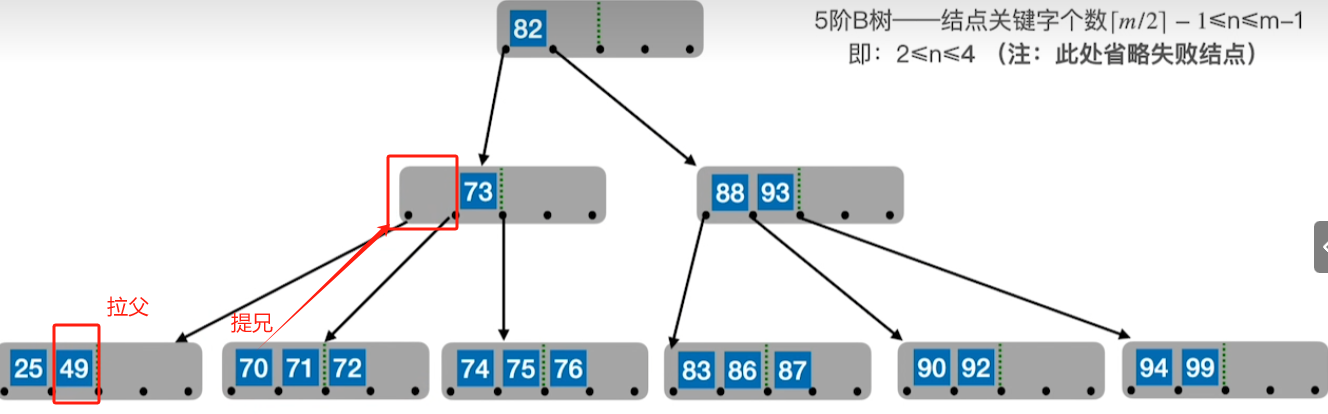
image-20241017001337664

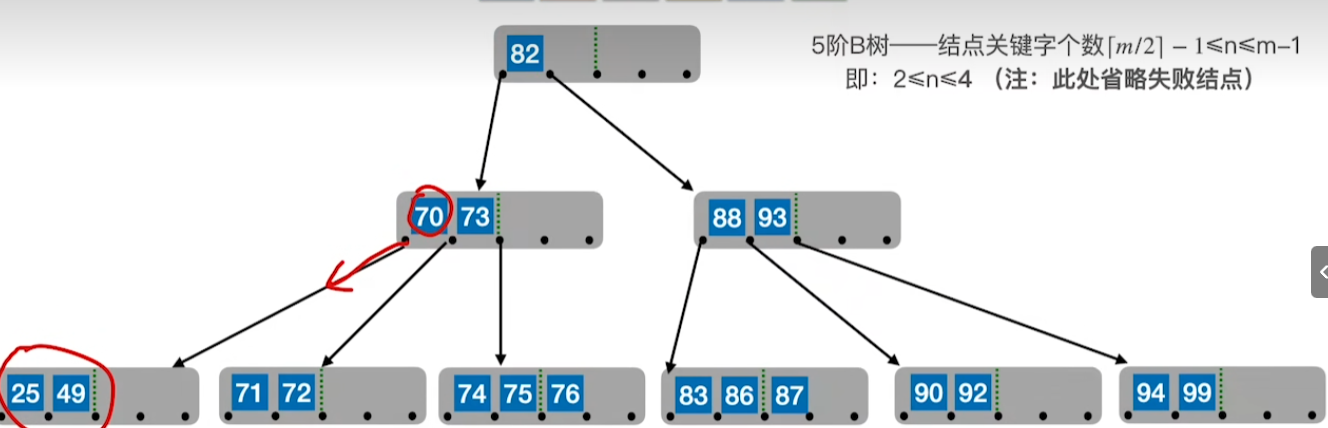
image-20241017001345969

image-20241017001402995

拉左兄弟

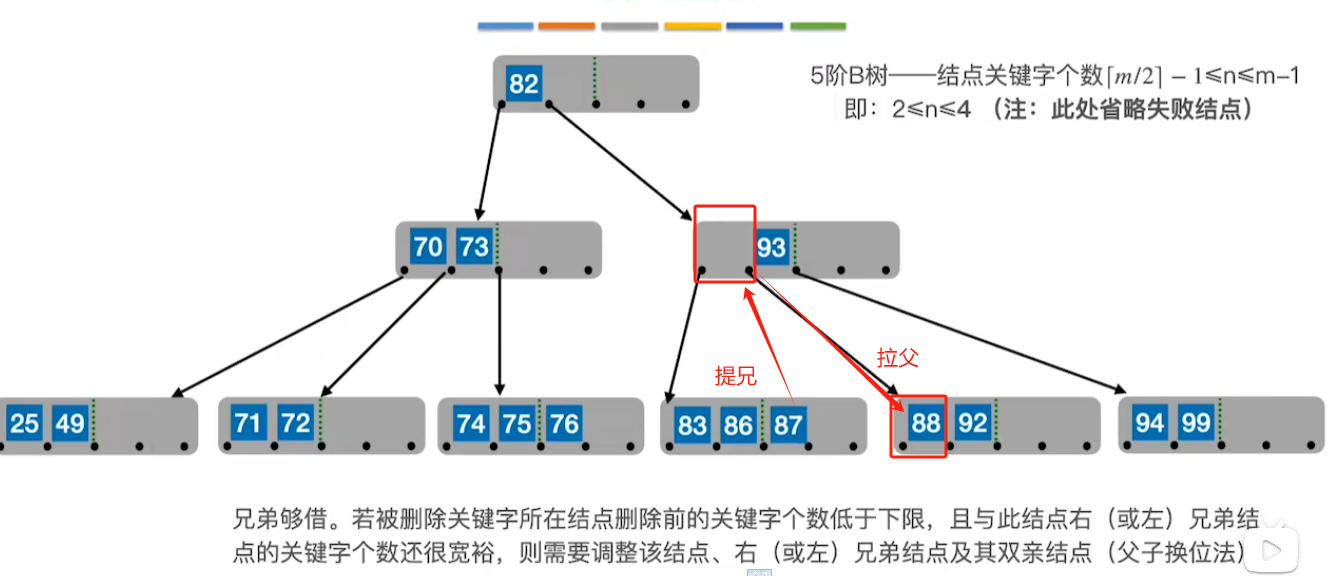
image-20241017001642875

image-20241017001655227

4、若被删除关键字在终端节点，且兄弟都不富裕，则进行合并操作

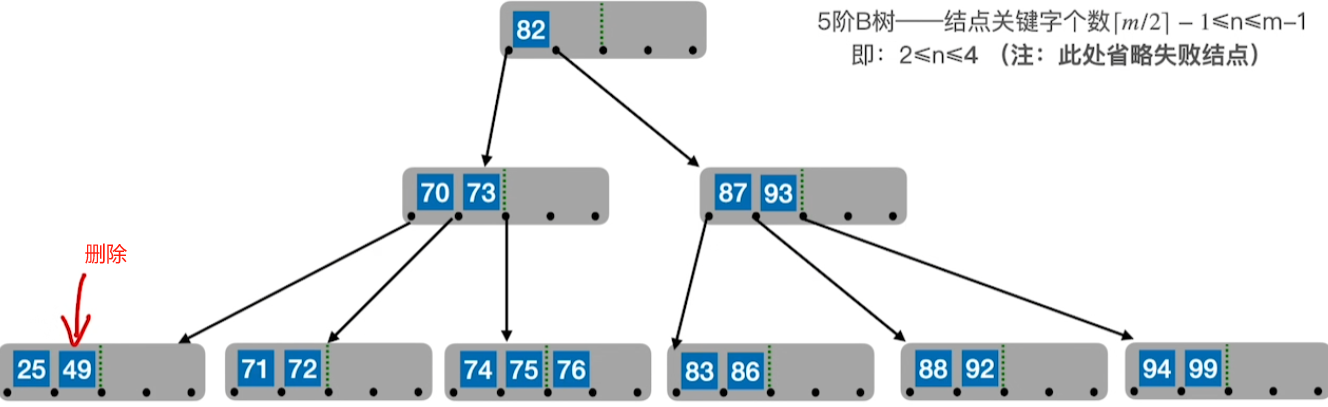
image-20241017002033596

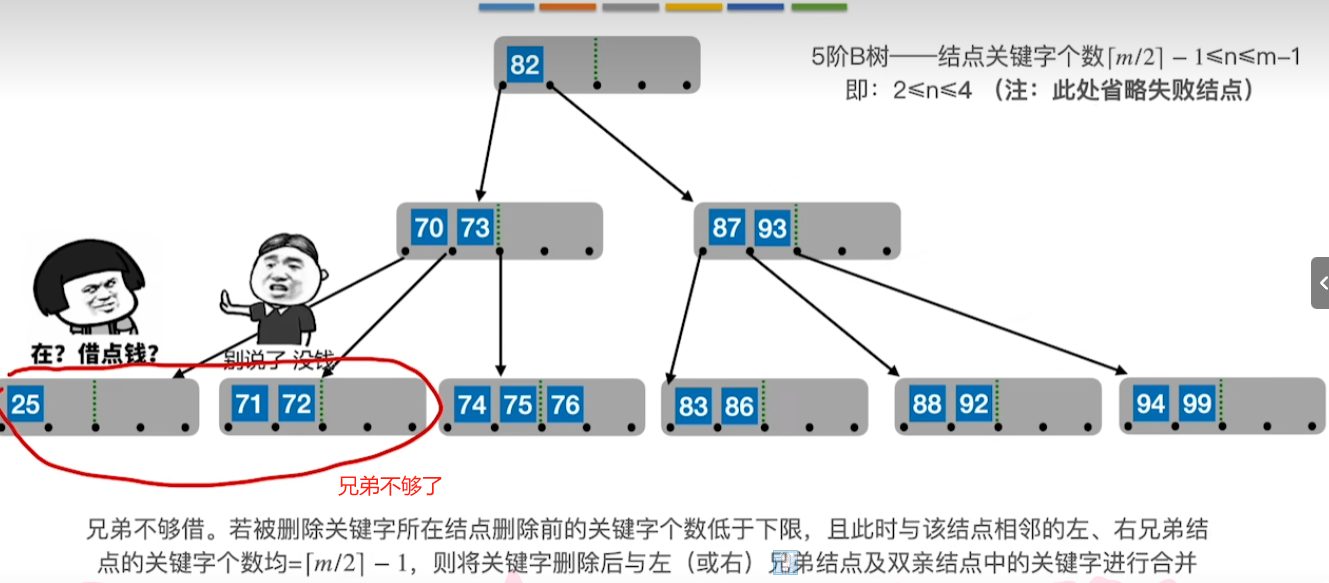
image-20241017002052910

合并操作

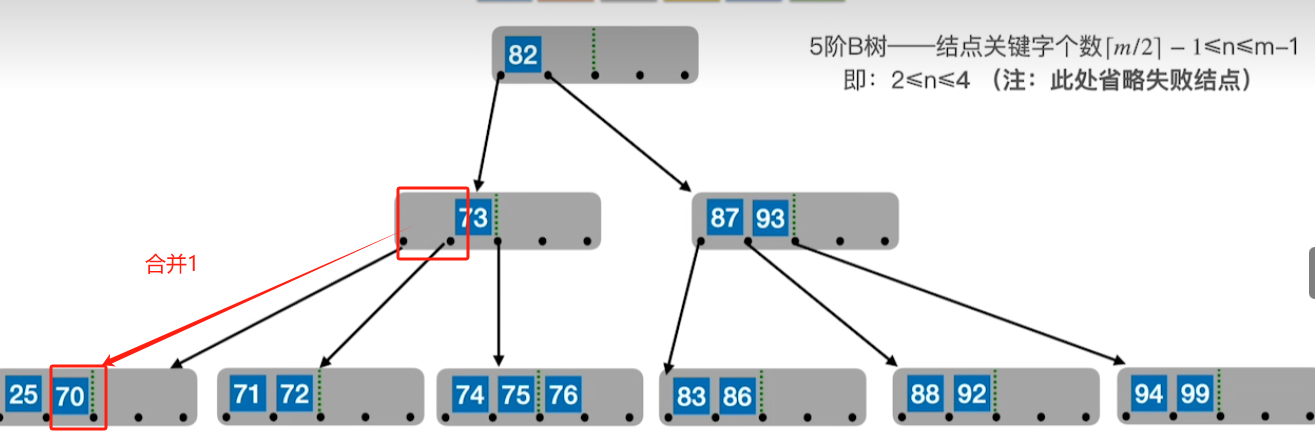
image-20241017002134567

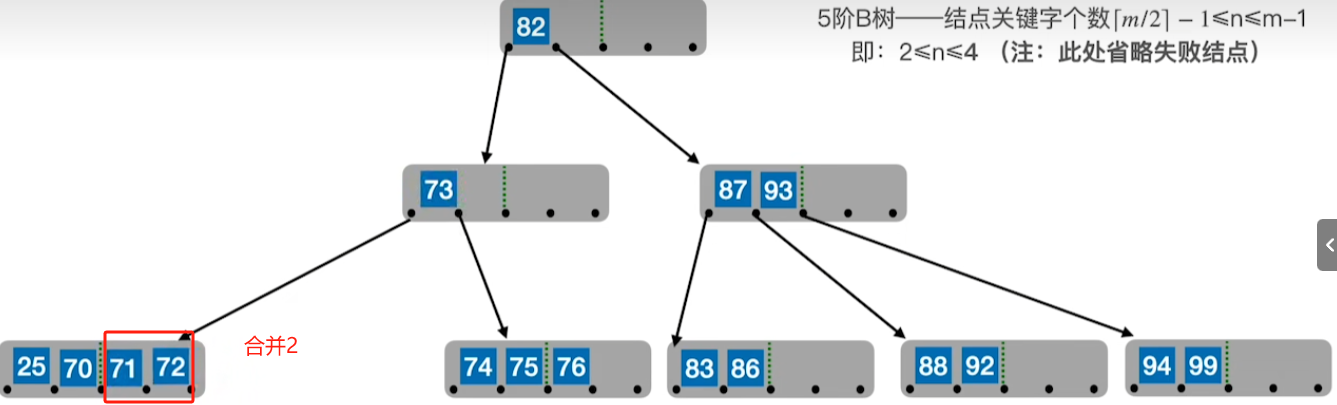
image-20241017002205170

若合并拉父后，父节点不满足B树，则继续进行拉父提兄，若兄依旧不足，则同样进行合并操作

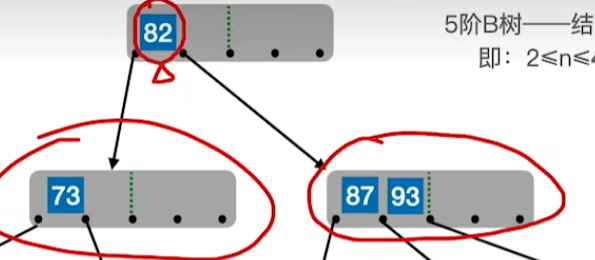
image-20241017002329095

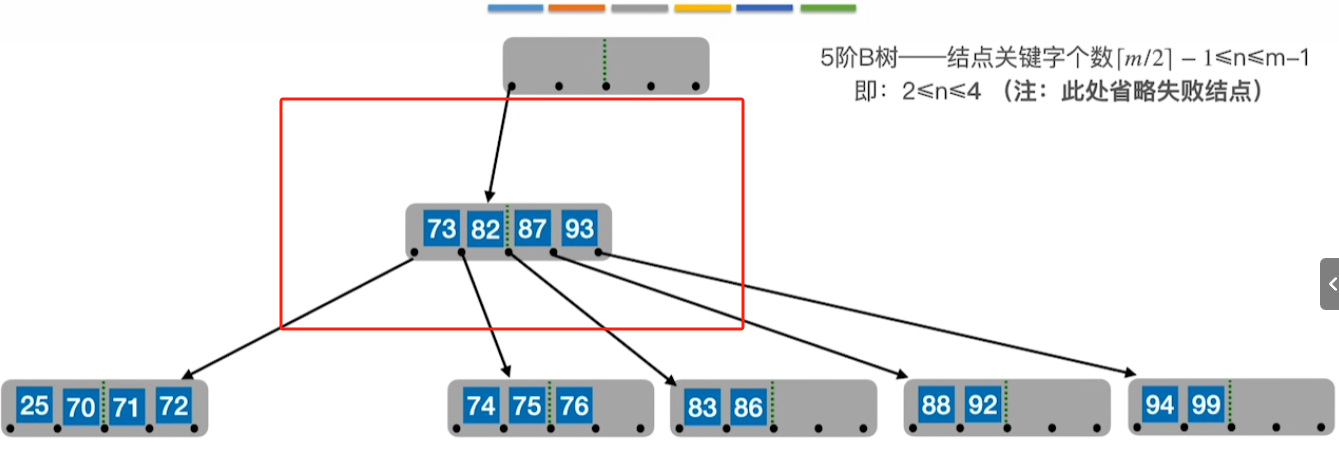
image-20241017002345193

image-20241017002358598

小总结

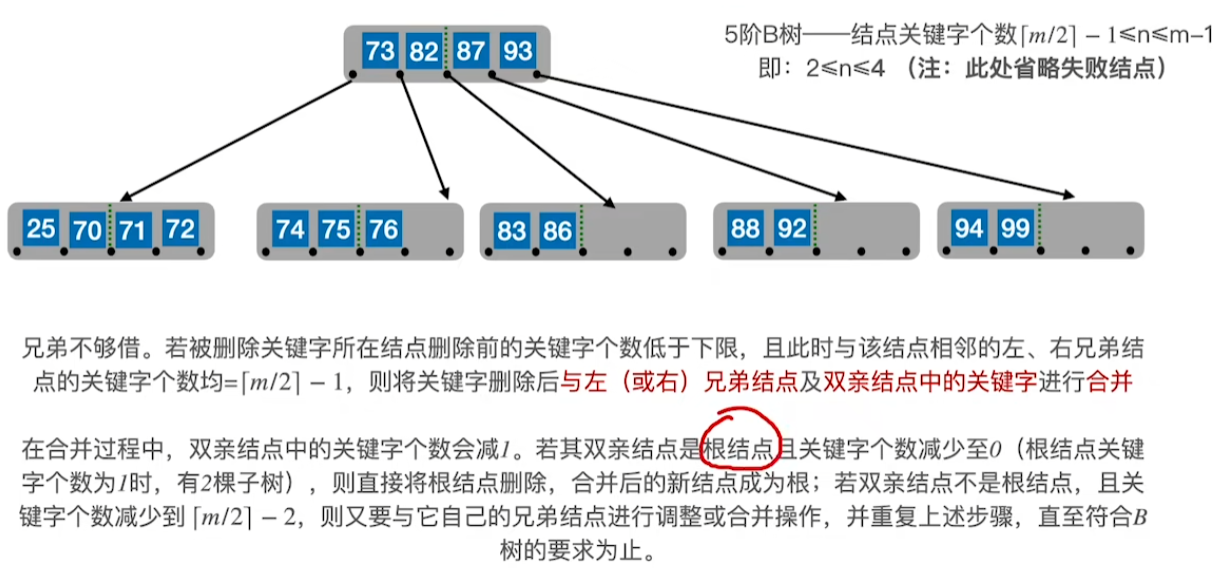
image-20241017002439058

插入删除操作总结

image-20241017001910348

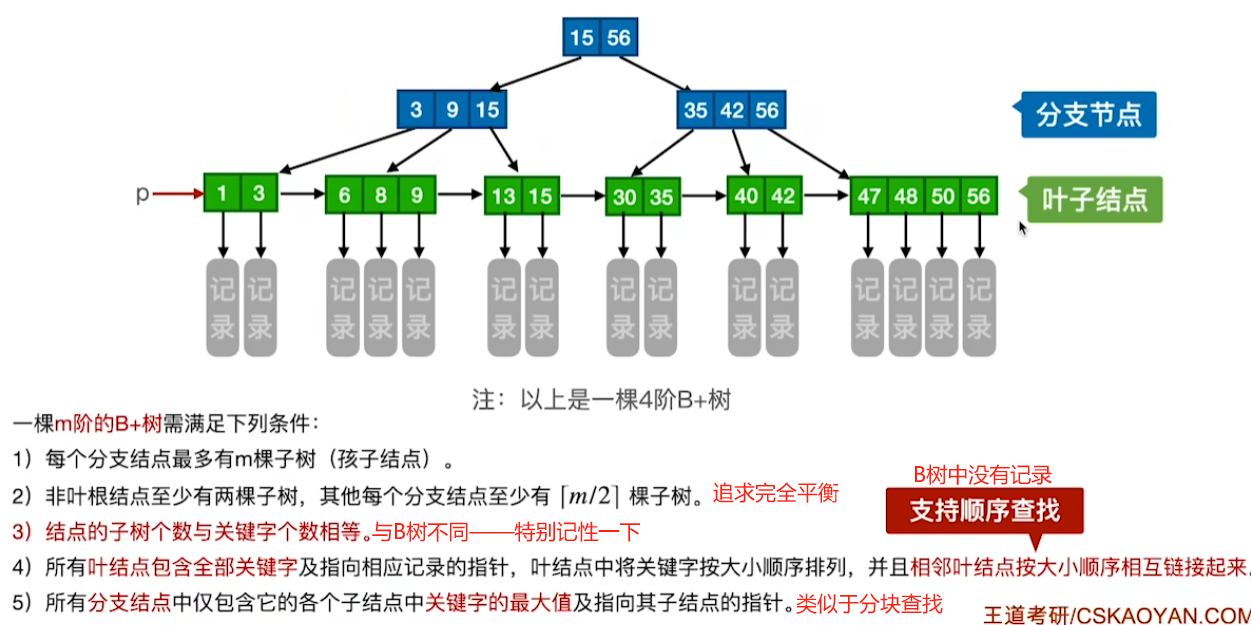
B+树

定义

类似于分块查找

image-20241017003151571

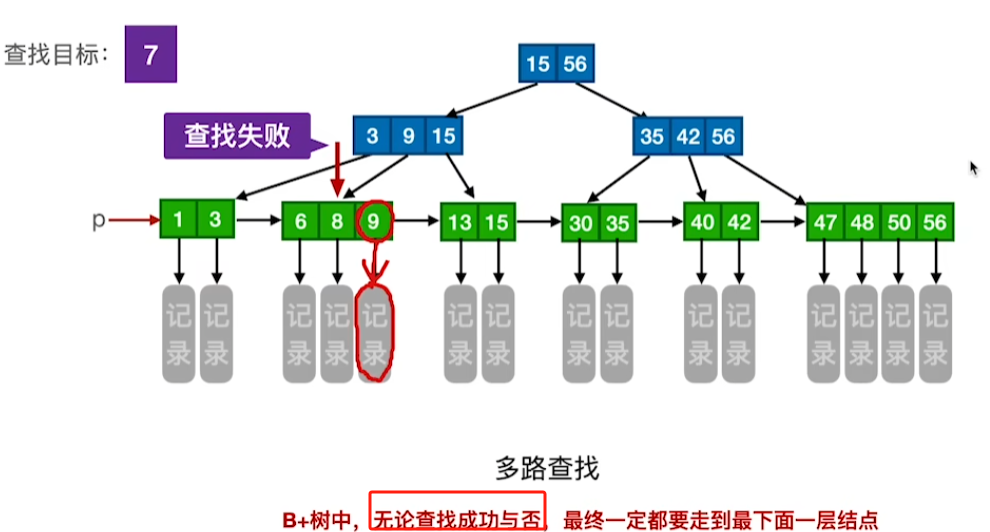
查找

多路查找

image-20241017003311320

顺序查找

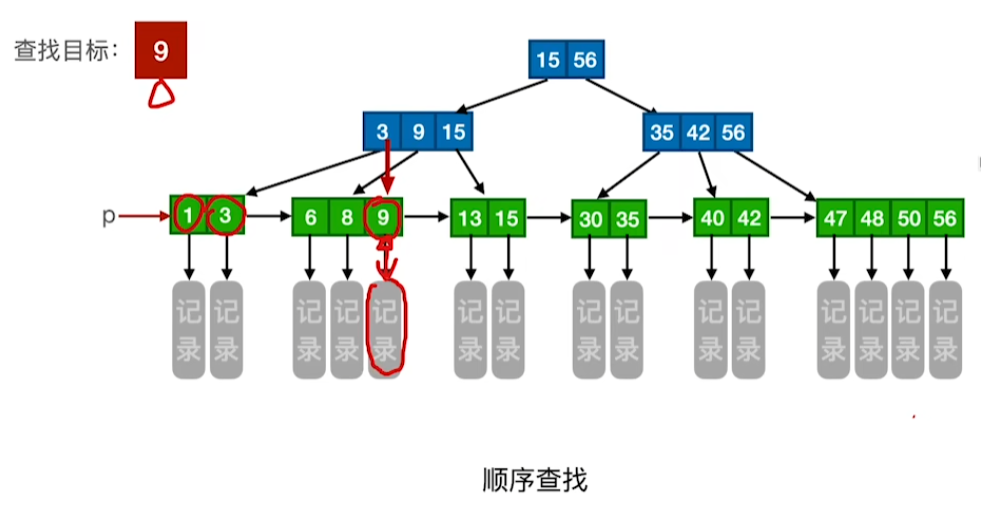
image-20241017003404496

对比B树

关键字对应分叉不同

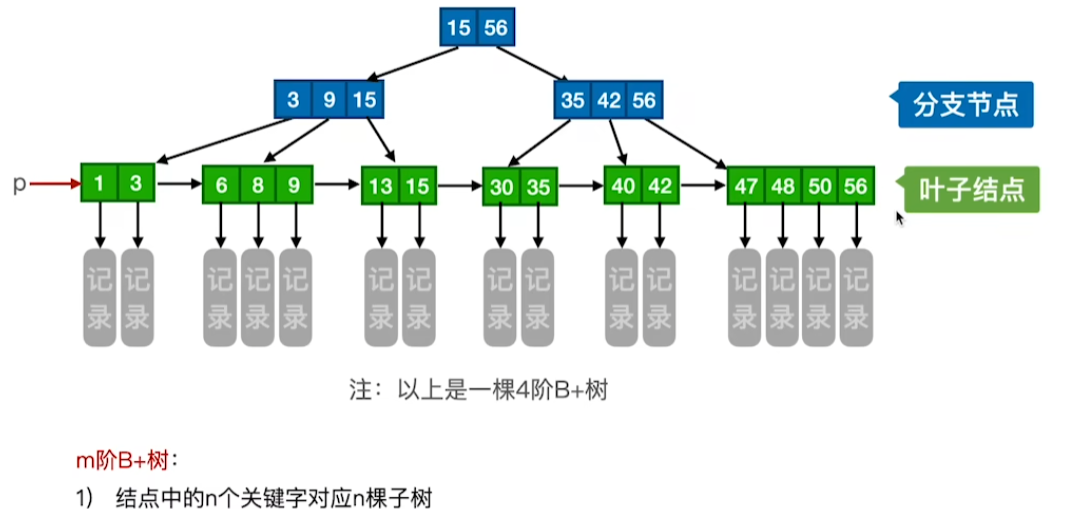
image-20241017003720421

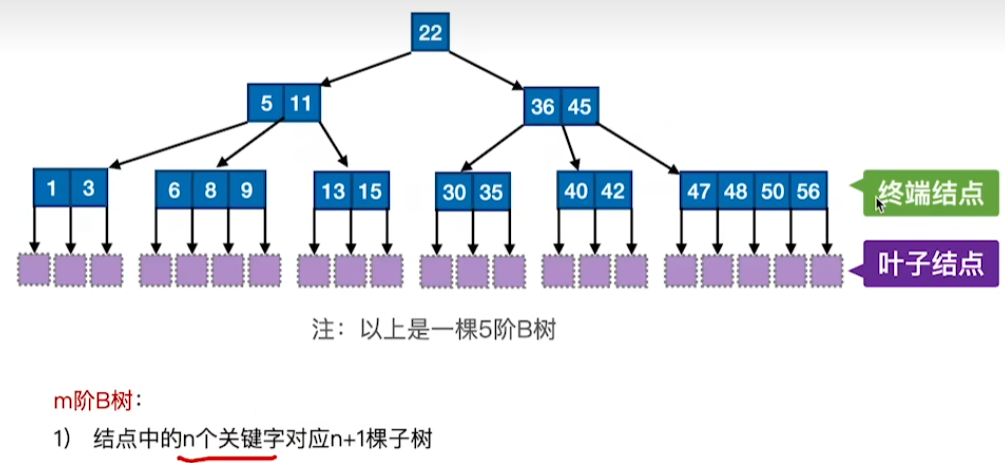
image-20241017003756331

节点关键字范围不同

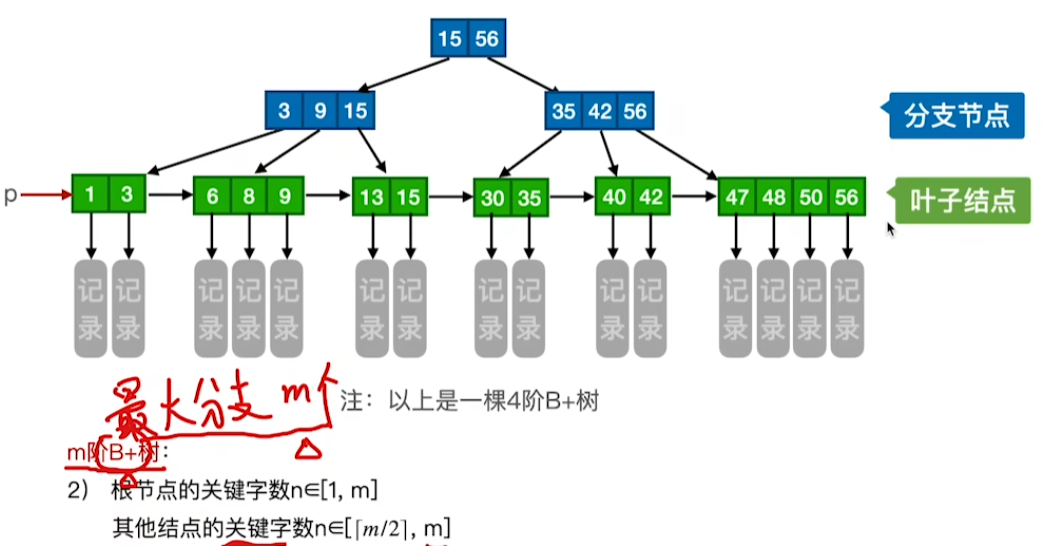
image-20241017003810669

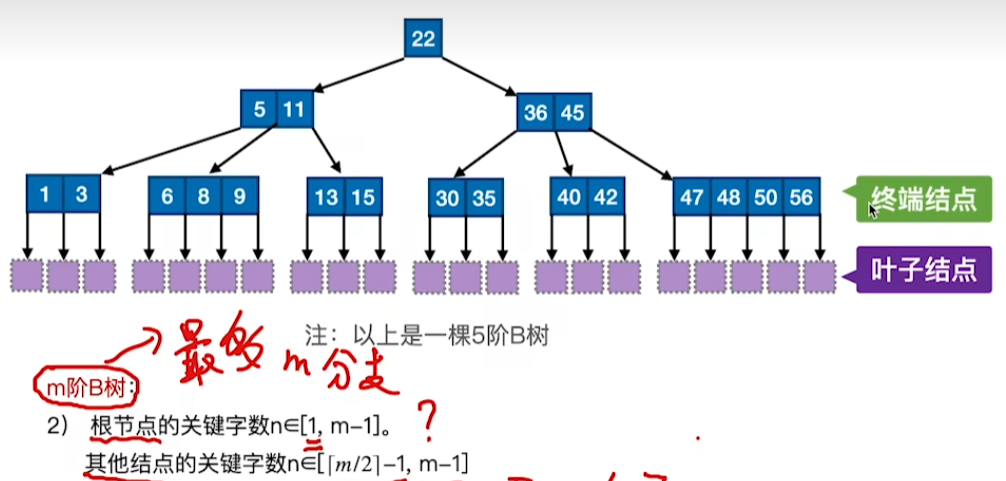
image-20241017003821400

叶子结点与关键字的关系

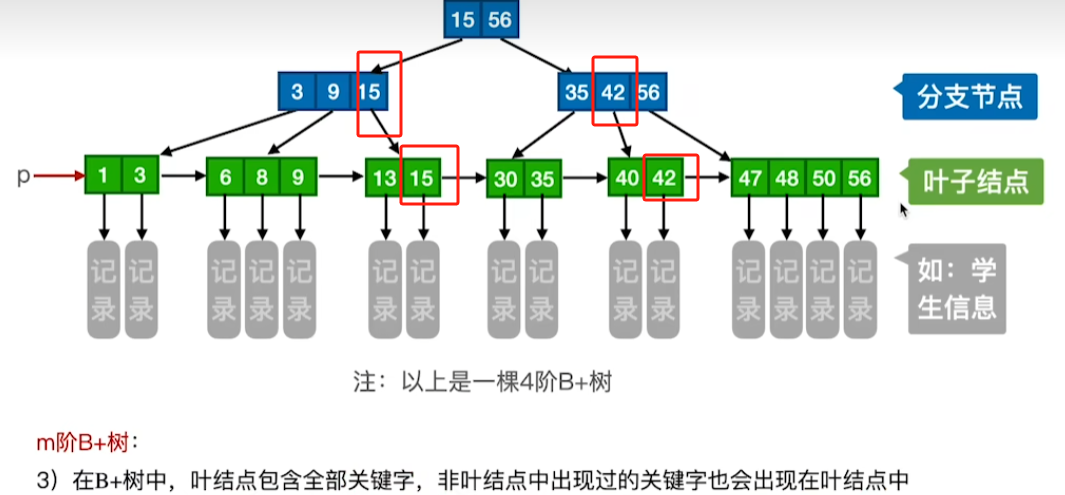
image-20241017003912731

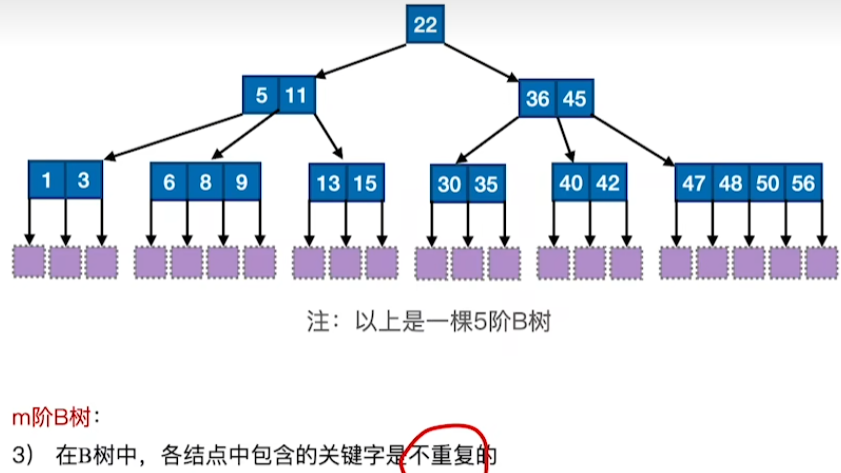
image-20241017003925235

节点作用

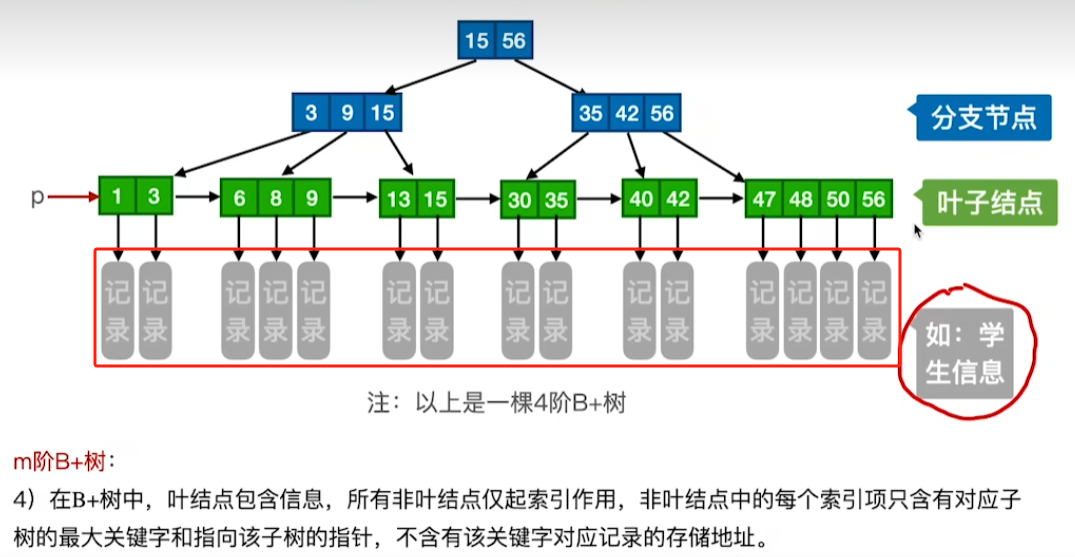
image-20241017003951671

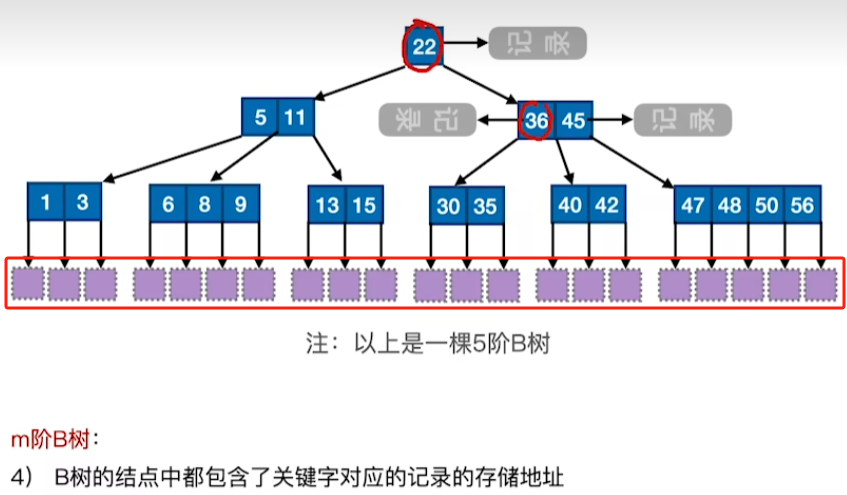
image-20241017004004516

存储本质区别

image-20241017004346727

总结对比

image-20241017004425394

散列查找（空间换时间）

概念

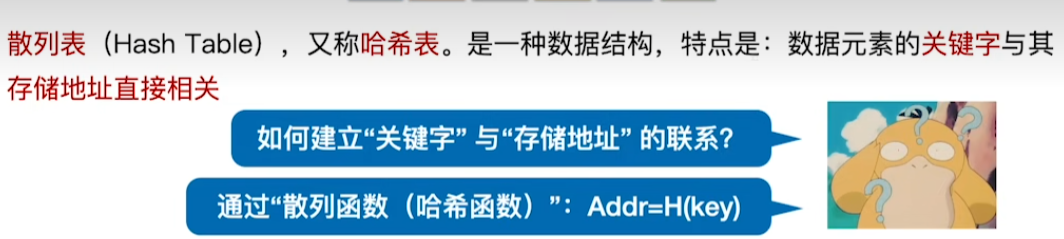
image-20241017004549079

散列函数

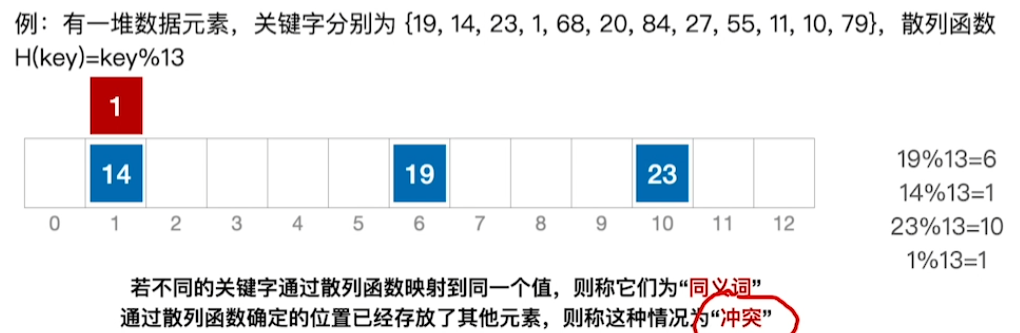
image-20241017004703834

ASL

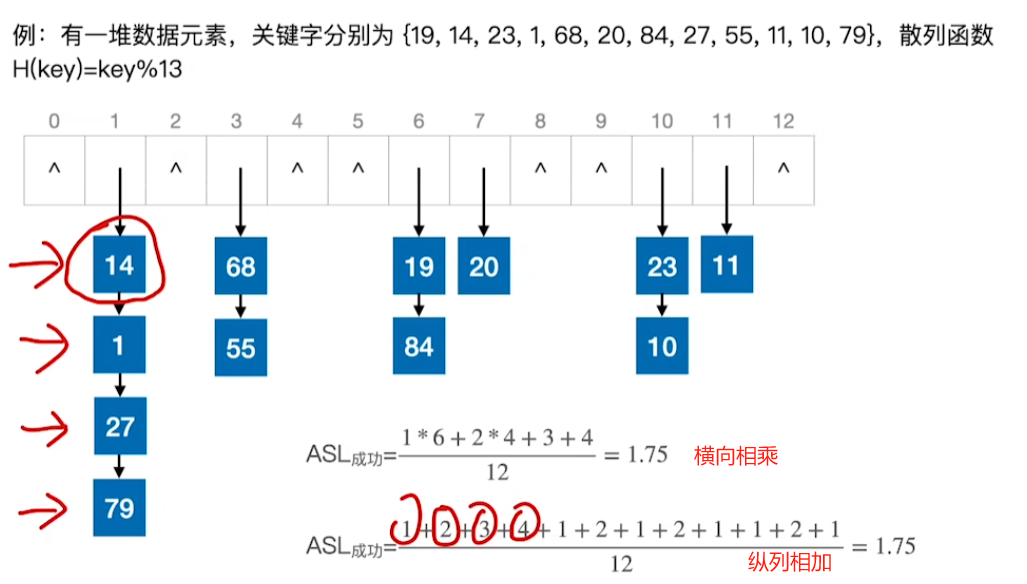
image-20241017005207221

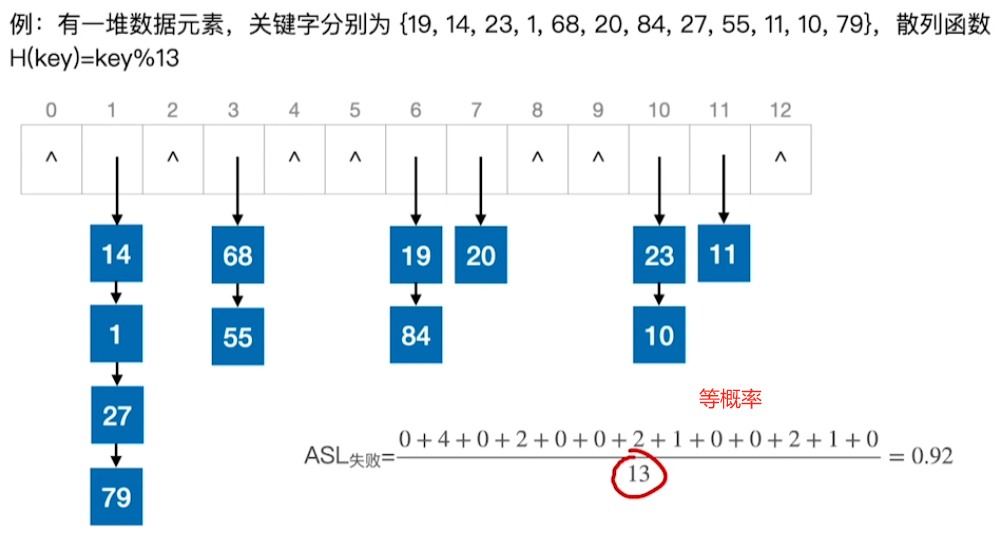
image-20241017005356091

装填因子

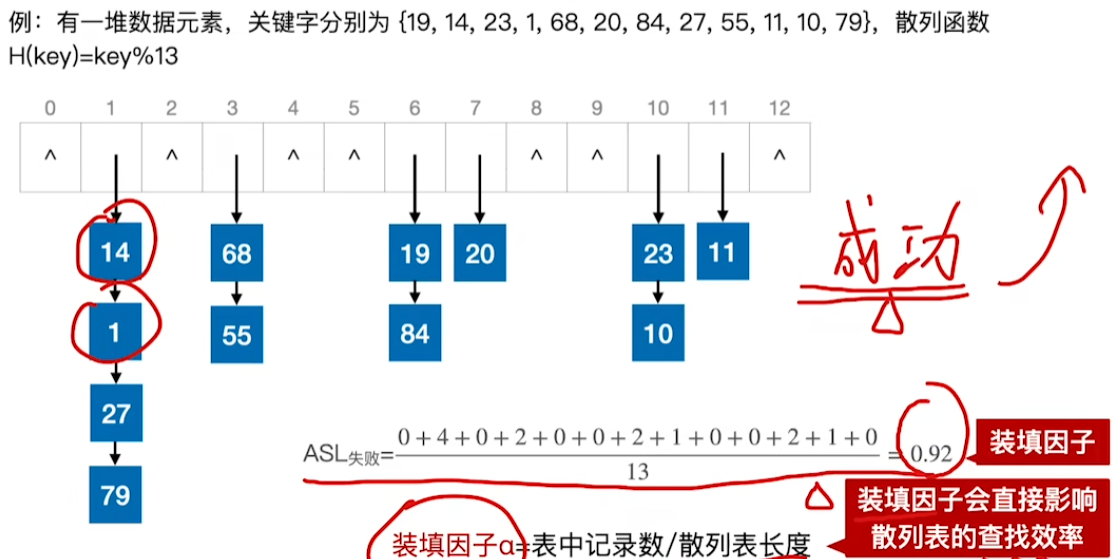
image-20241017005505987

常见散列函数设计方法（哈希函数）

除留余数法

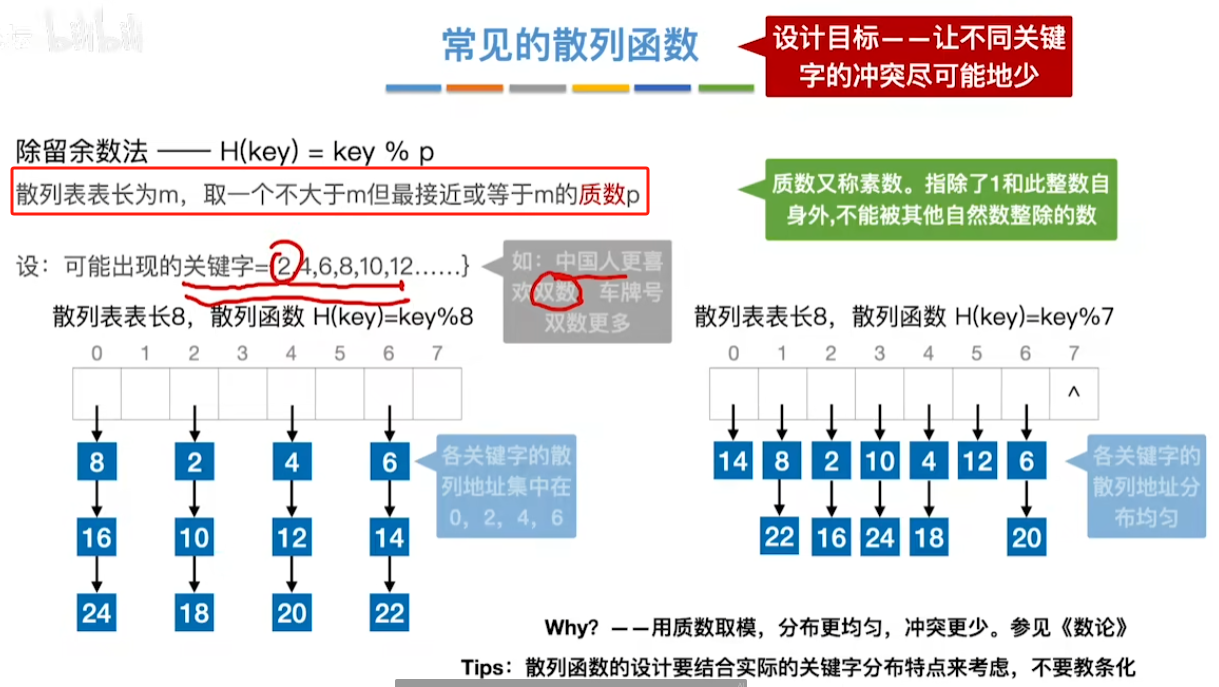
image-20241017005938195

直接定址法

image-20241017010055682

数字分析法

image-20241017010139572

平方取中法

image-20241017010323937

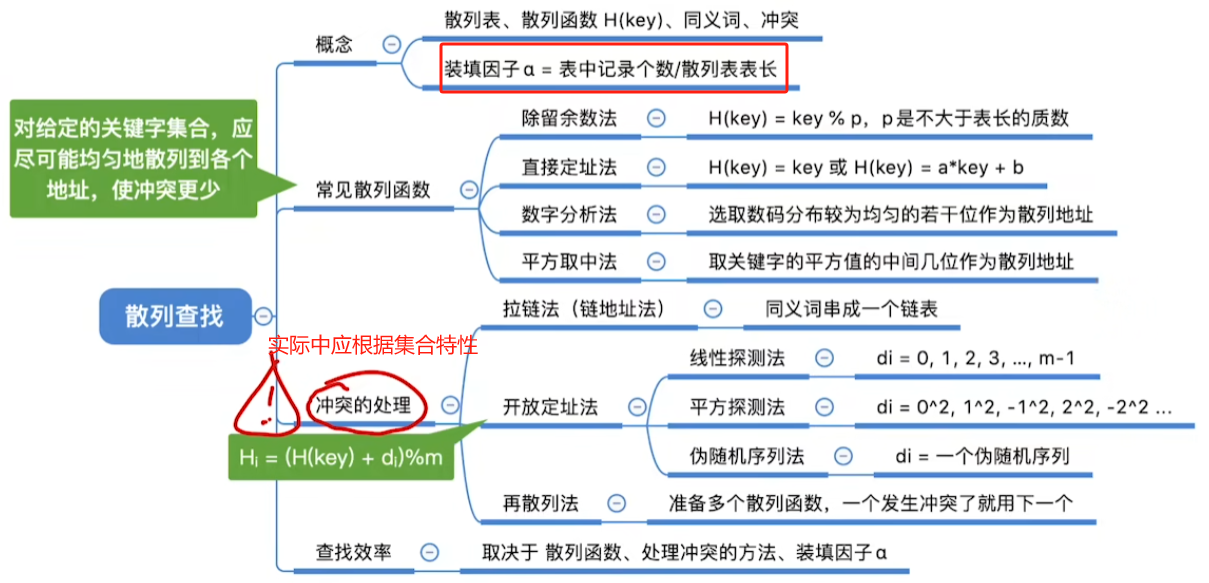
处理冲突方法

拉链法

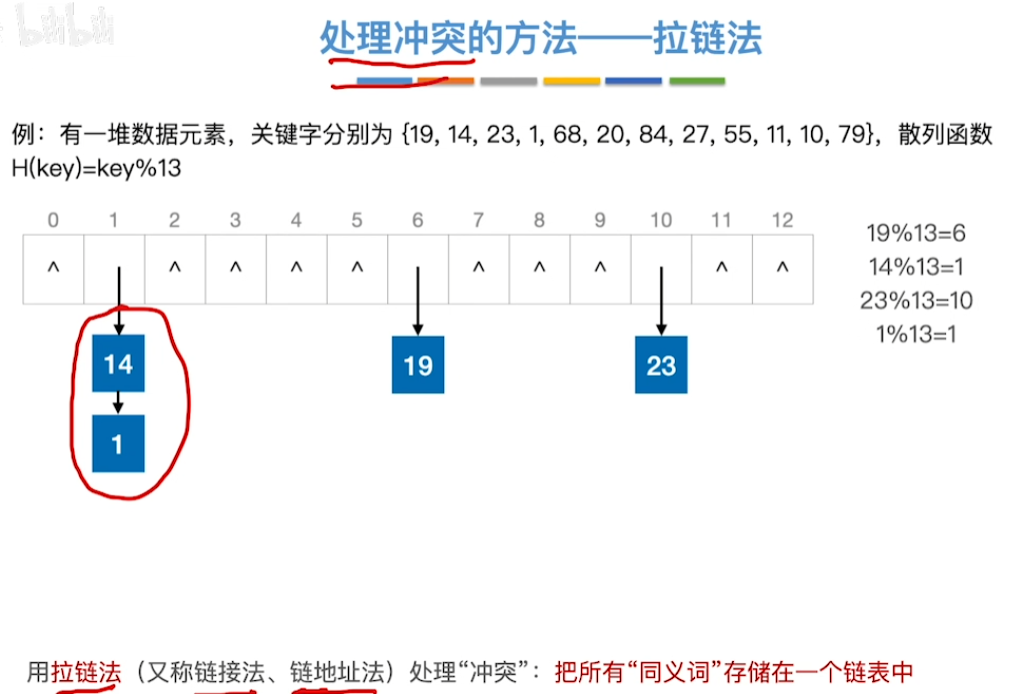
image-20241017004733011

开放定址法

image-20241017010633101

线性探测法

探测该位置后续位置是否有冲突

image-20241017010816319

image-20241017011736753

查找操作

image-20241017011853919

删除操作

image-20241017011813942

平方探测法

image-20241017012101117

image-20241017012133495

伪随机序列法

image-20241017012324271

再散列法（再哈希法）

image-20241017012436895

总结

image-20241017012636241

排序算法与数据结构

插入排序

原理

将每个元素前面的所有更大的元素往后移，将该元素移到比该元素大的元素的最前面，即逐次前移

image-20241018002246997

代码实现

image-20241018002511098

也可以带哨兵

image-20241018002553794

时间复杂度

image-20241018003002098

image-20241018003047727

image-20241018003057259

优化——折半查找

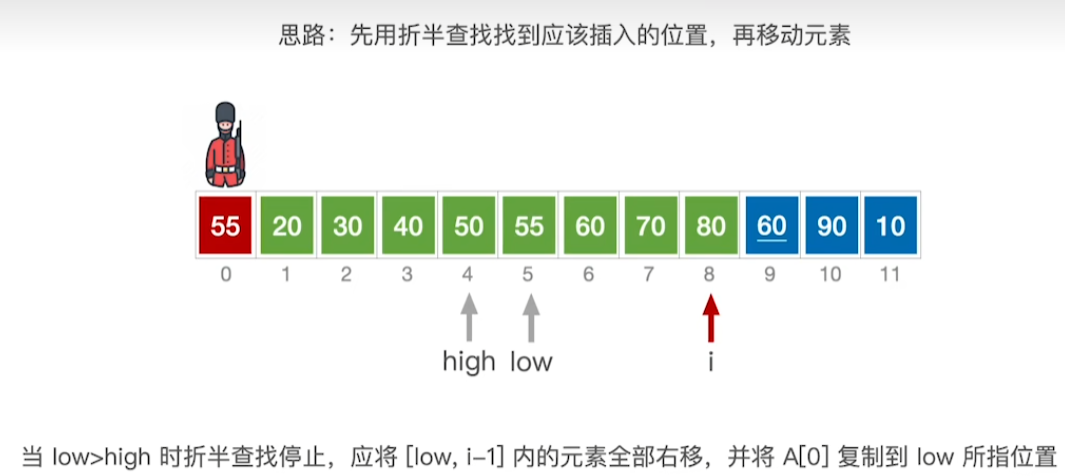
image-20241018003233796

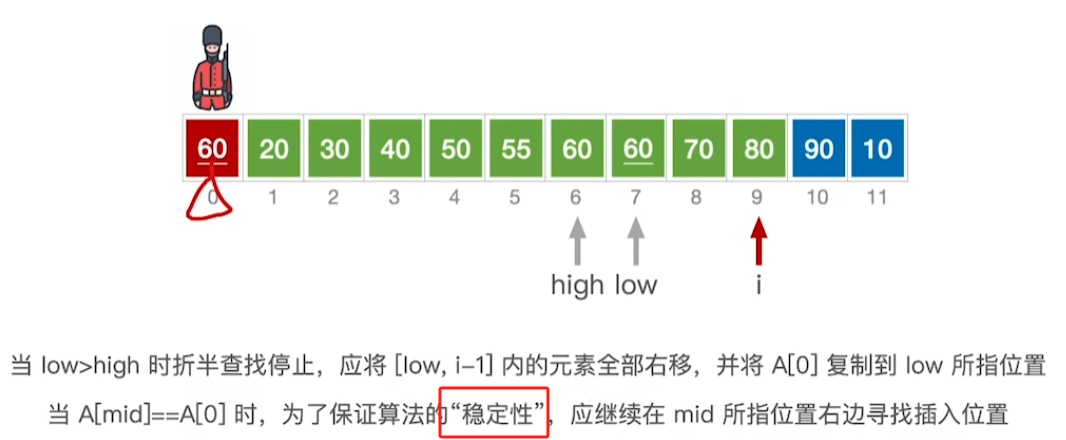
image-20241018003408680

优化代码实现

image-20241018003628460

时间复杂度

image-20241018003649640

总结

image-20241018003740405

希尔排序

定义

image-20241020173527781

原理

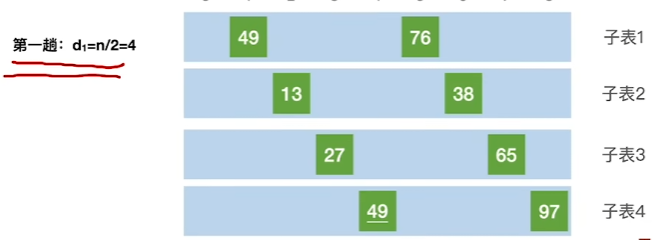
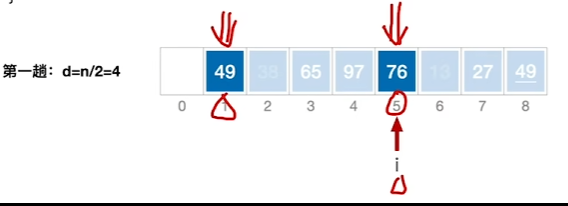
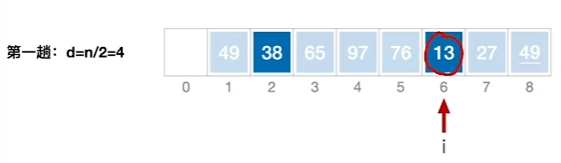
1、对一个序列进行排序，加入一个增量d，进行多趟排序，d表示两个元素之间的距离

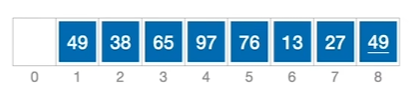
image-20241020173612489

2、进行第一趟排序，找到增量对应的子表，对每一个子表进行一次插入排序

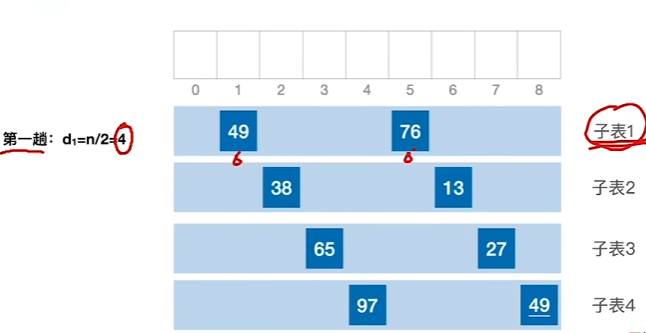
image-20241020173710727

image-20241020173752141

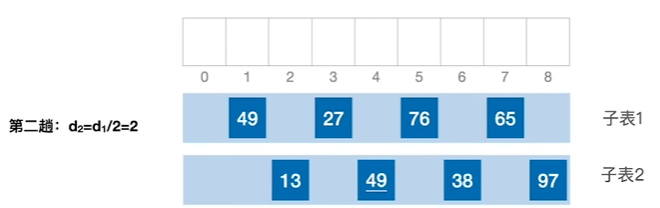
2、进行第二趟处理

image-20241020173832119

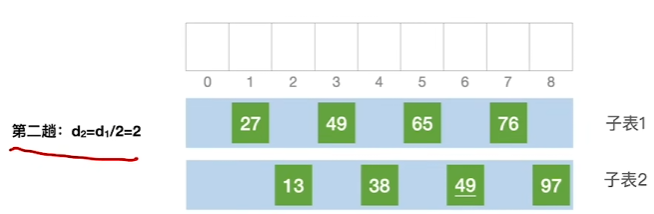
image-20241020173841981

3、进行第3趟处理

image-20241020173857632

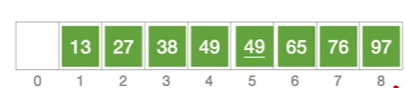
image-20241020173911992

综合

image-20241020173938544

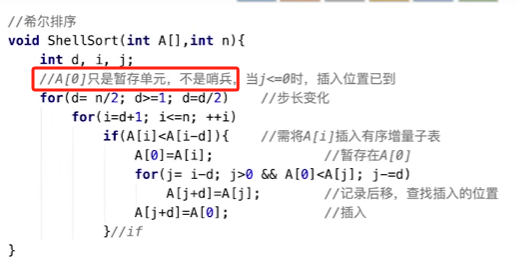
代码实现

从中间往后选择元素，并选择在其之前的子表

image-20241020174058044

image-20241020174141470

image-20241020174151976

image-20241020174241603

时间复杂度与空间复杂度

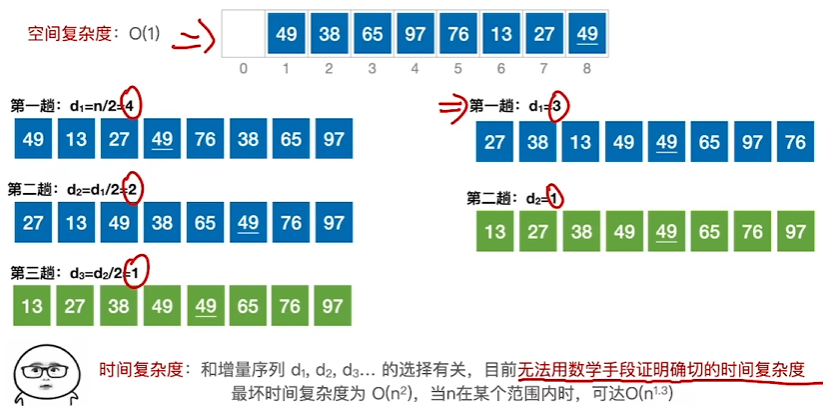
image-20241020174451785

稳定性与适用性

image-20241020174538889

总结

image-20241020174557762

交换排序

冒泡排序

原理

每一趟都两两比较互换位置，每一次选出一个最小（最大）的数，需要进行n-1趟，每一趟需要比较（n-当前趟次）的数

image-20241020174700091

算法实现

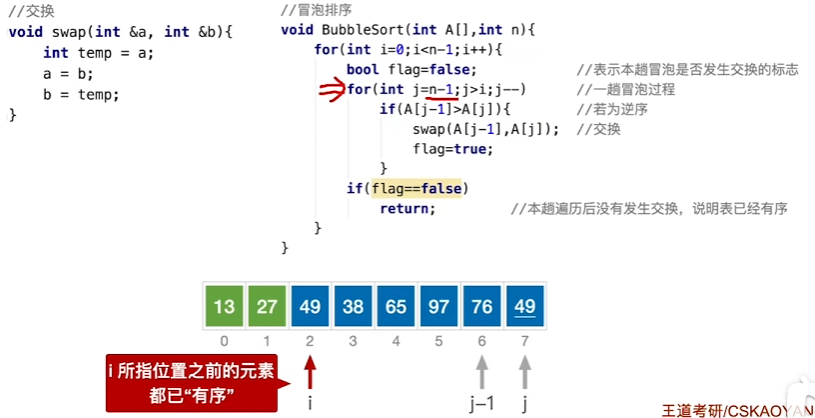
image-20241020174906709

时间复杂度与空间复杂度

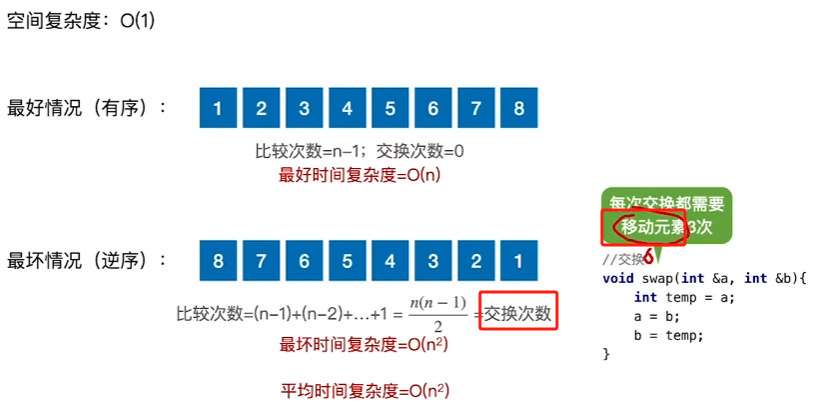
image-20241020175502397

总结

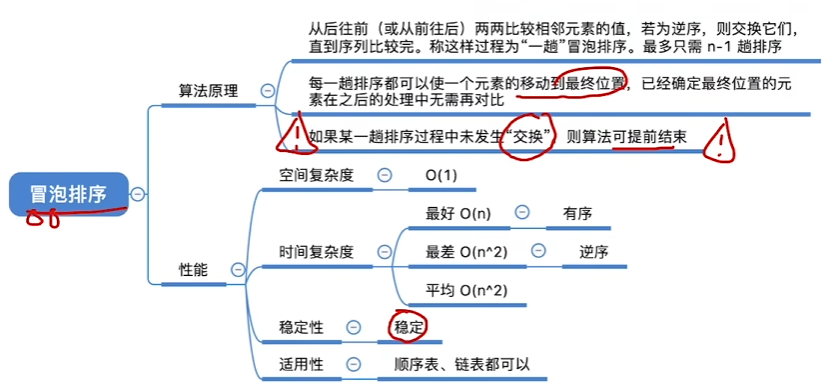
image-20241020175544566

快速排序（最快）

定义

image-20241020175644250

原理

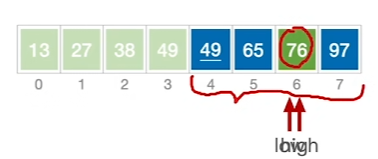
选择每一块的基准进行递归排序，基准元素一般选取子表的第一个元素

1、选择基准，将其他数进行左右分配

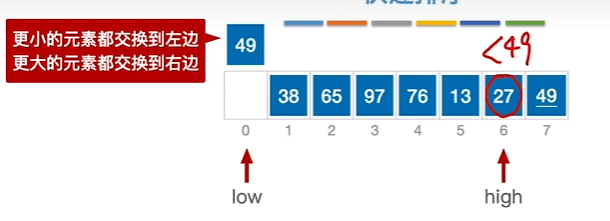
image-20241020175754458

2、当low、high指针相遇，确定基准元素位置

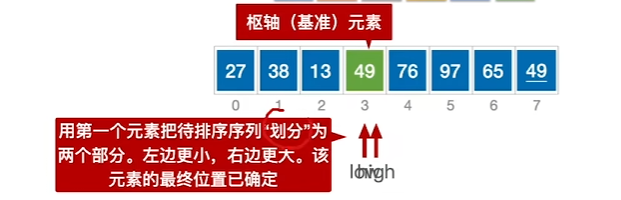
image-20241020175809579

3、递归对左右子表进行基准划分

左子表

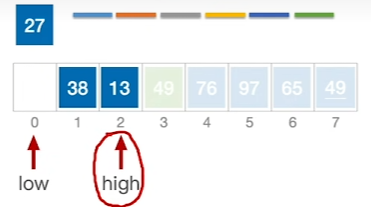
image-20241020175858540

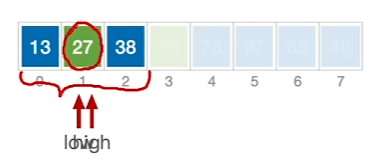
image-20241020175907492

右子表

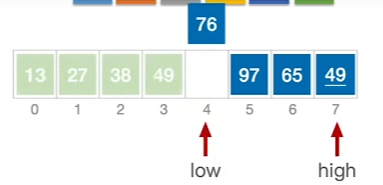
image-20241020175927680

image-20241020175945154

算法实现

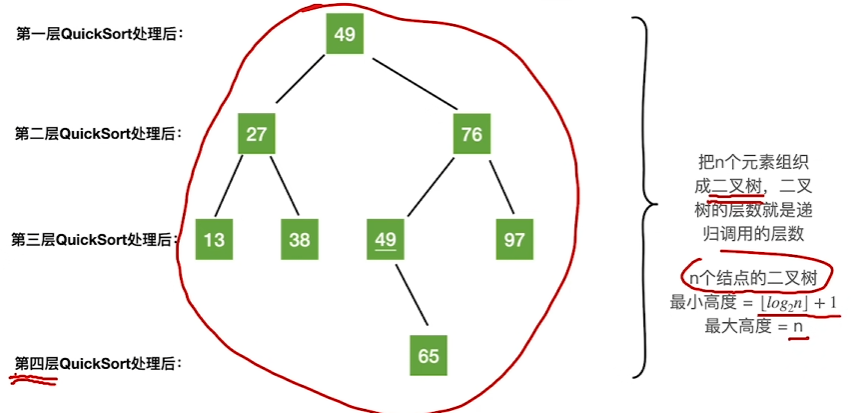
需要用到函数递归调用栈（但时间复杂度忽略不计）

image-20241020180057465

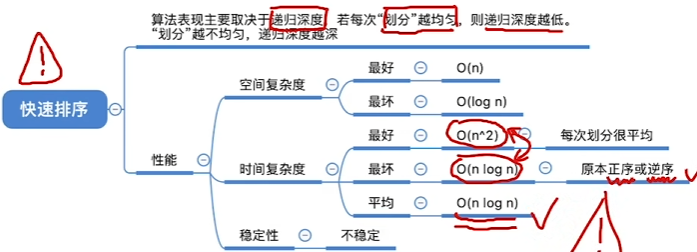
时间复杂度与空间复杂度

image-20241020180216798

image-20241020180338804

image-20241020180319219

总结

image-20241020180400472

选择排序

简单选择排序

定义

image-20241020180530734

原理

对未进行排序的元素进行选择一个最小（最大）的元素，并将其放入有序子序列

image-20241020180648361

代码实现

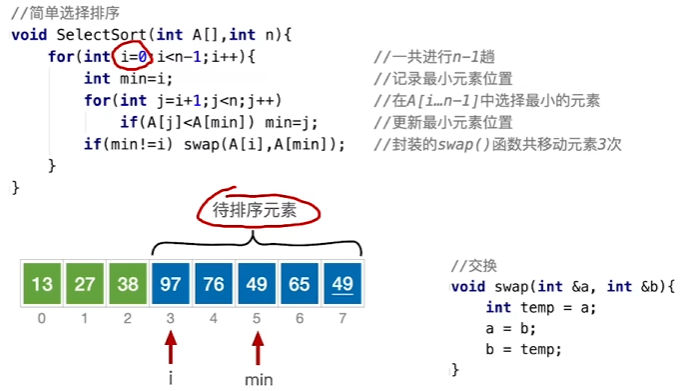
image-20241020180707185

时间复杂度与空间复杂度

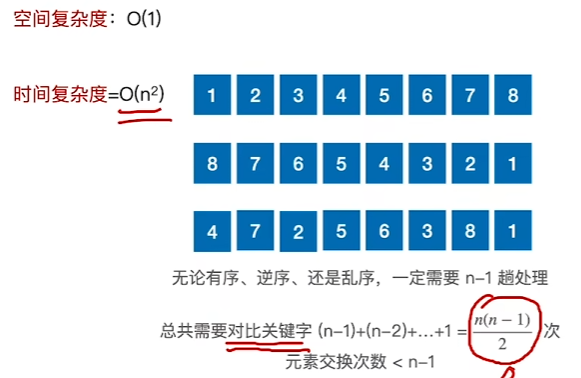
image-20241020180734893

总结

不会因为原序列初始状态而改变时间复杂度

image-20241020180757459

堆排序

定义堆

image-20241020180843383

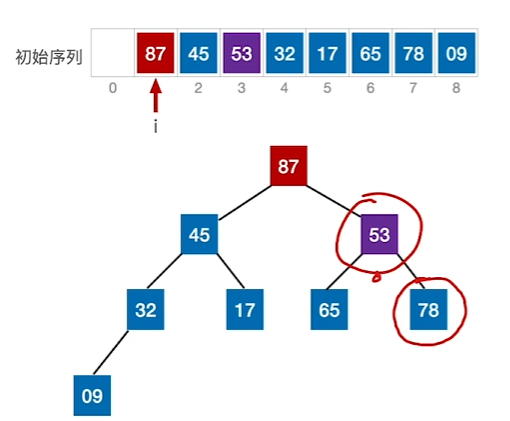
大根堆：即所有根节点大于其所有左右子树的结点

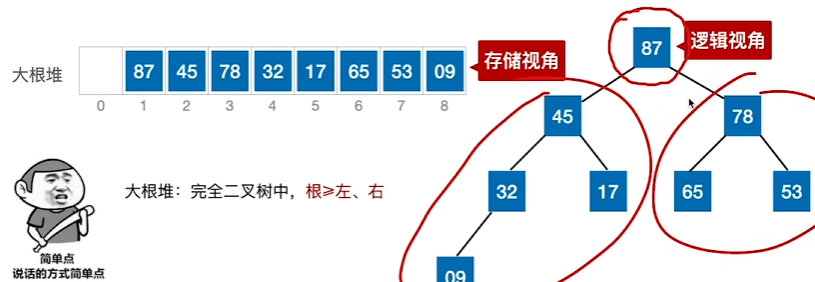
image-20241020180934164

小根堆：即所有根节点小于其所有左右子树的结点

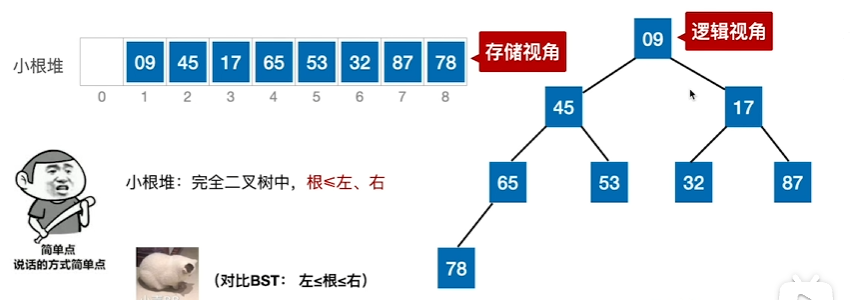
image-20241020181015029

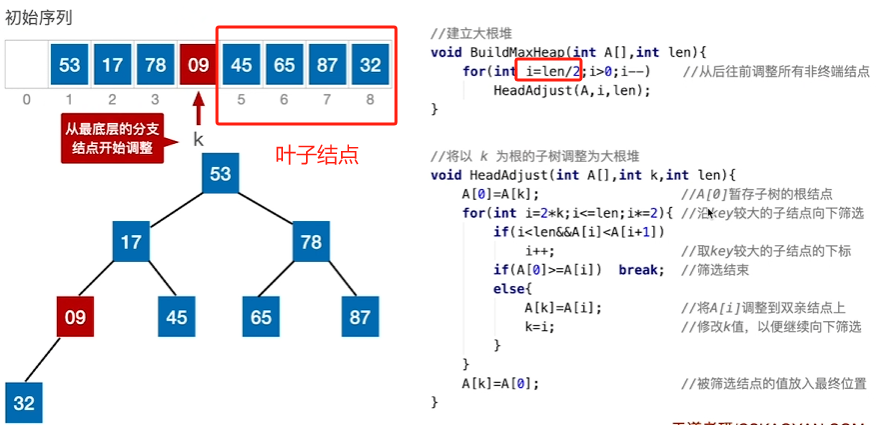
建立大根堆

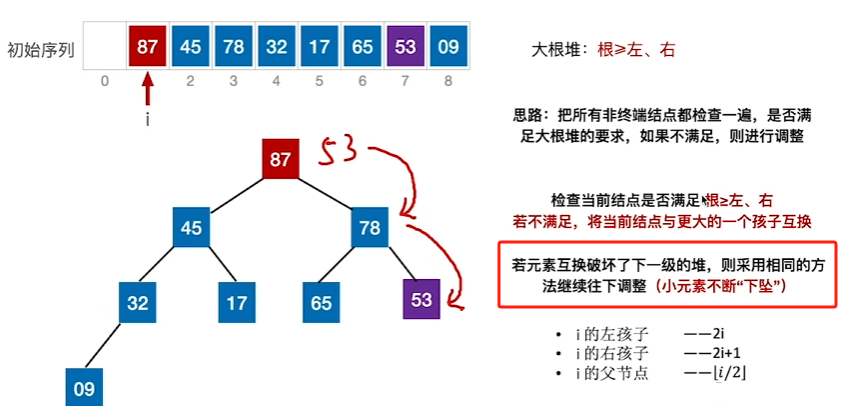
1、找到序号最大（后续一次减小）的根结点，比较看是否满足大根堆，不满足则替换

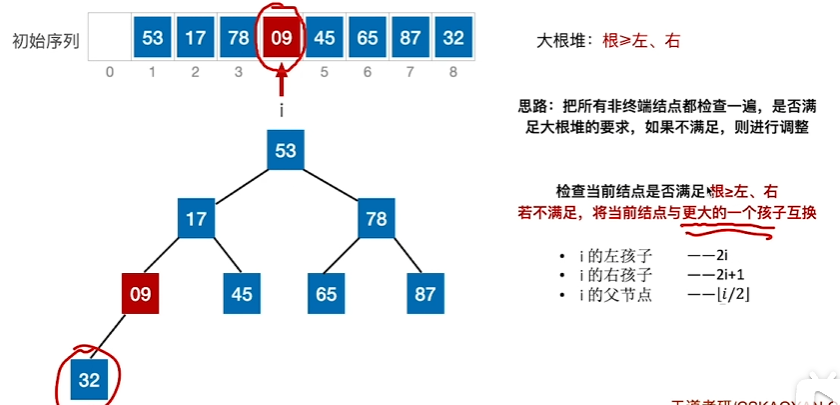
image-20241020181148582

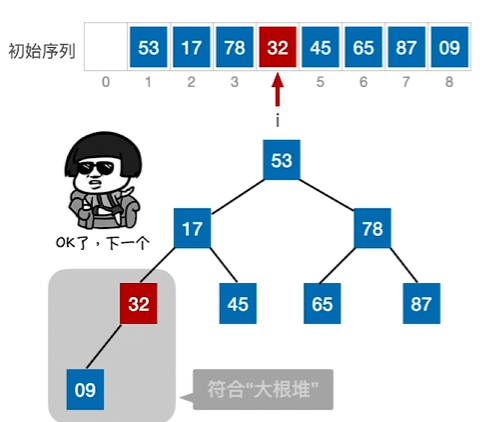
image-20241020181206890

2、找到序号倒数第二大的根结点，比较看是否满足大根堆，不满足则替换

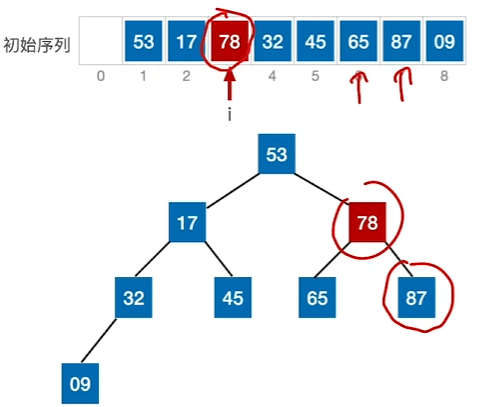
image-20241020181253591

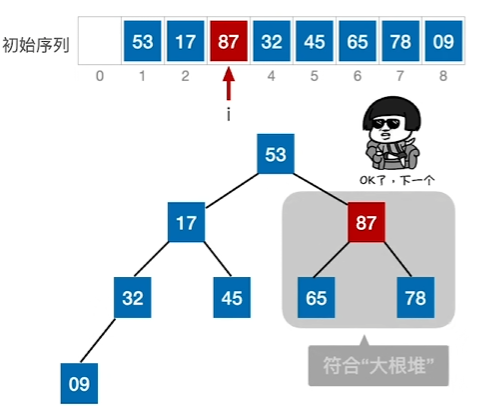
image-20241020181259591

3、当出现更小的元素“下坠”时，进行向下调整，直至无法下调

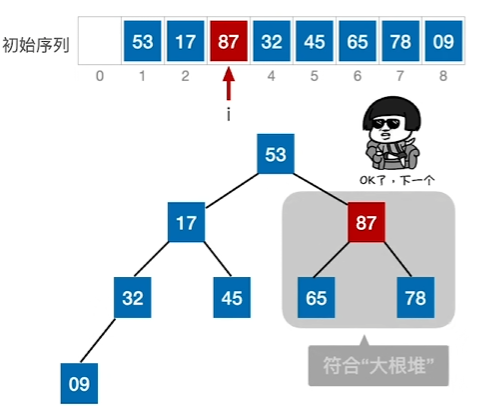
image-20241020181343406

image-20241020181410488

image-20241020181428820

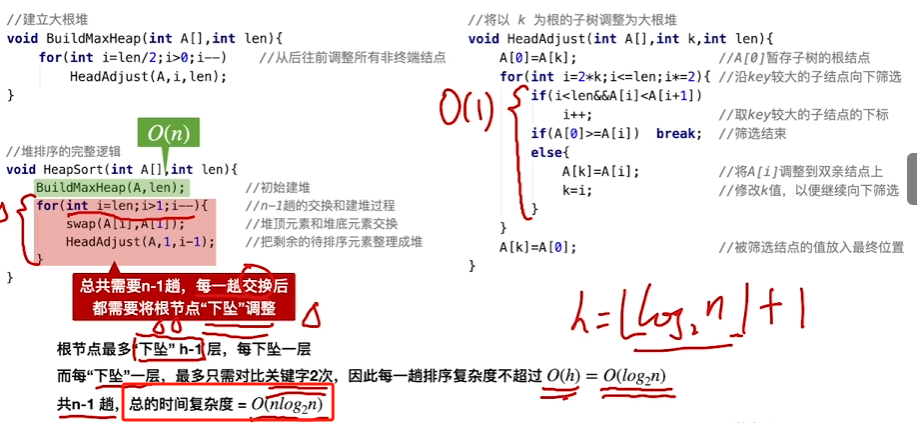
代码实现

image-20241020181517498

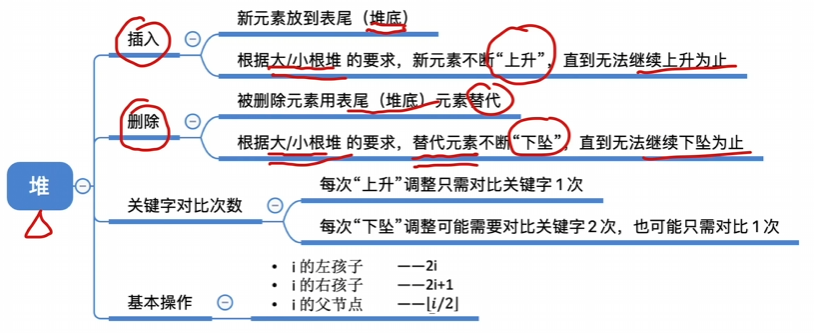
堆的插入与删除

image-20241020182302499

基于大根堆排序
原理

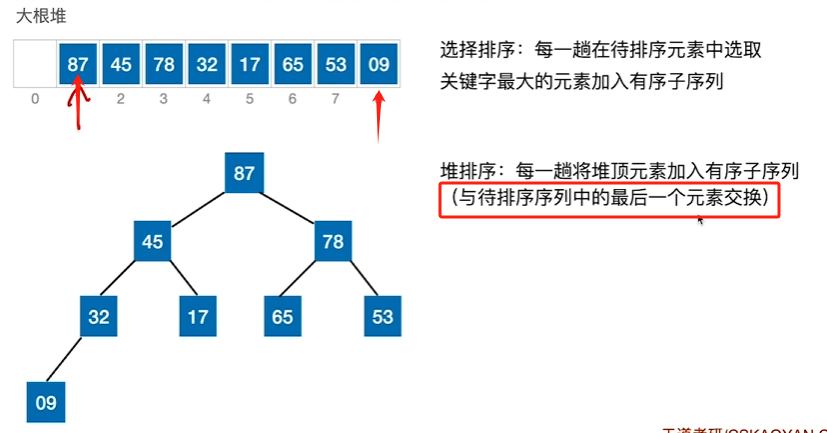
image-20241020181642989

最大的87已被移除大根堆

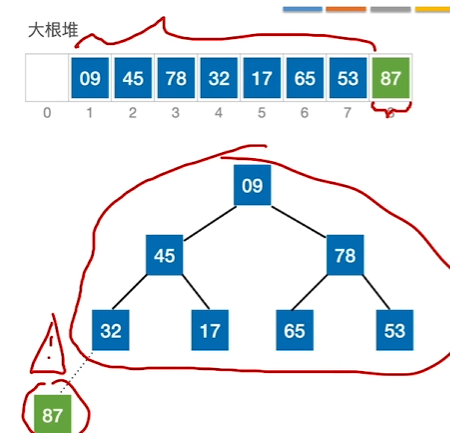
image-20241020181652702

调整，使让09不断下坠

image-20241020181728736

代码实现

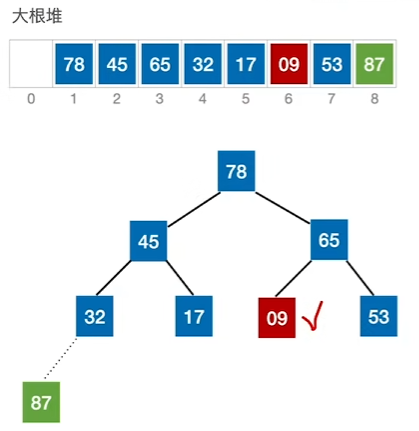
移除后再建立新堆

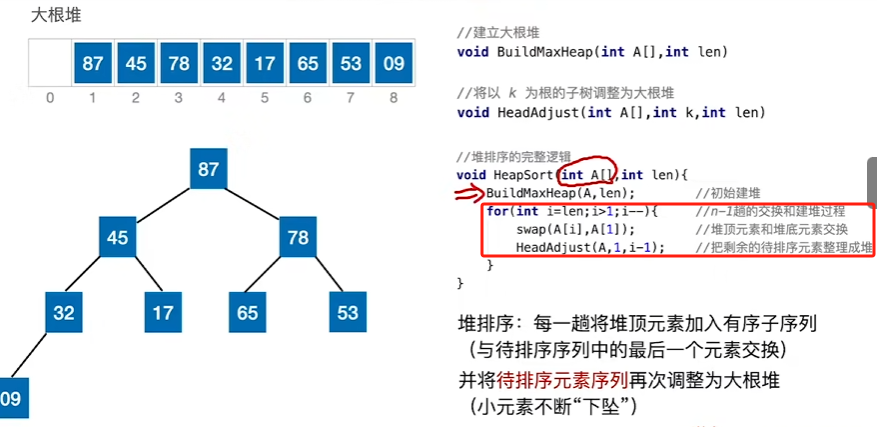
image-20241020181830123

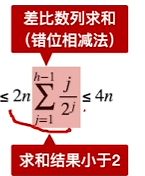
时间复杂度与空间复杂度

image-20241020181959296

image-20241020182021994

image-20241020182030525

image-20241020182107136

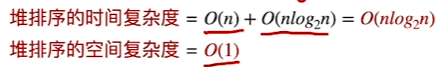
image-20241020182113995

总结

image-20241020182207698

归并排序

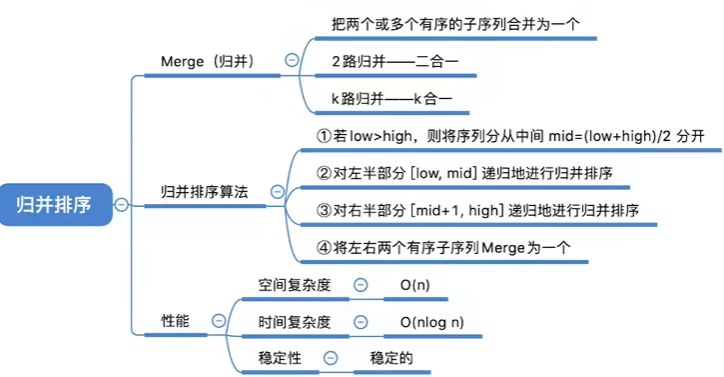
定义

把两个或多个已经有序的序列合并成一个（递归）

（二路）

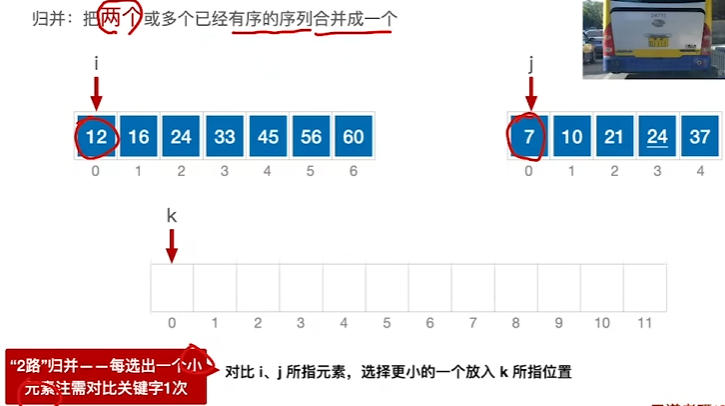
image-20241021010312292

（四路）

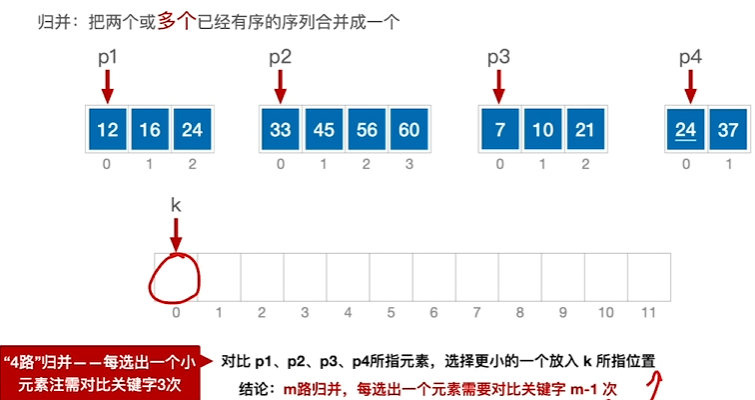
image-20241021010410434

原理（二路）

1、将序列中两两归并

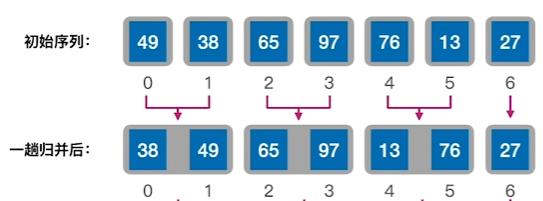
image-20241021010458285

2、将序列中两两归并后的两组两两归并

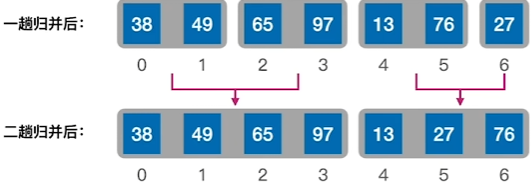
image-20241021010522076

3、将两组归并后的4个1组的再进行归并，最后得到一个完整的序列

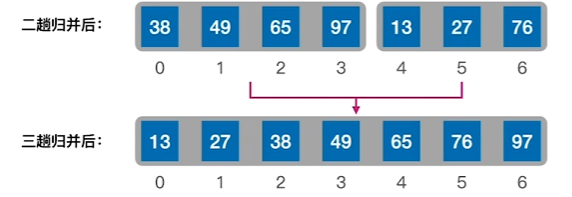
image-20241021010549182

代码实现

使用一个数组进行全部复制，使用两个指针进行对原数组的复写

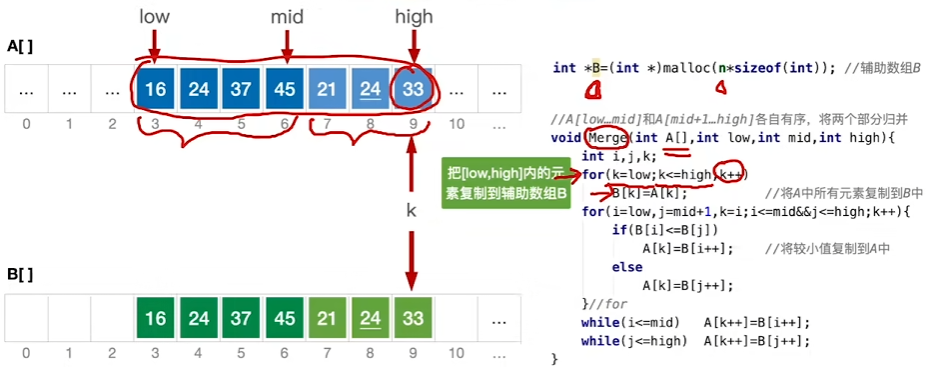
image-20241021010707967

image-20241021010801115

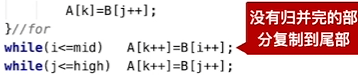
image-20241021010831273

完整代码（递归）

image-20241021010857453

时间复杂度与空间复杂度

image-20241021011133937

总结

image-20241021011156860

基数排序

定义

image-20241021011901032

（不基于关键字进行对比，而是对其关键字的每一位数进行对比然后排序）

原理

1、对数字的个位进行分配（首次无需管顺序）

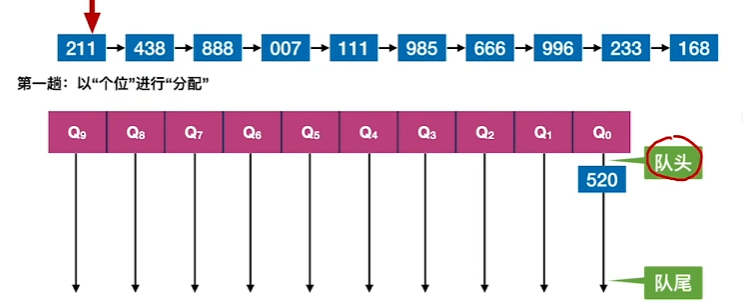
image-20241021011258543

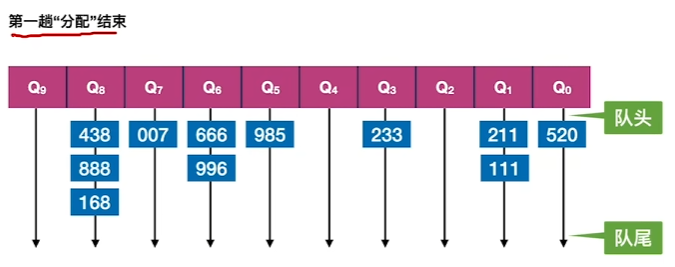
image-20241021011308089

2、对第一次分配的进行收集（从前往后连成一条新的序列）

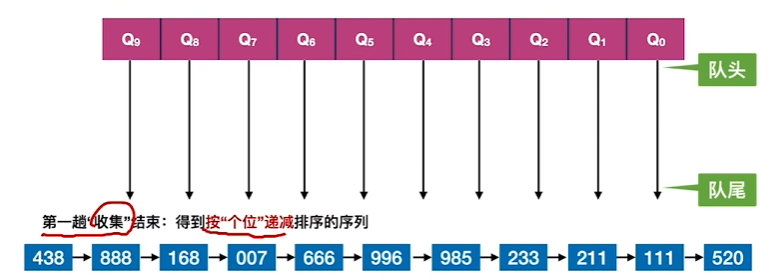
image-20241021011358871

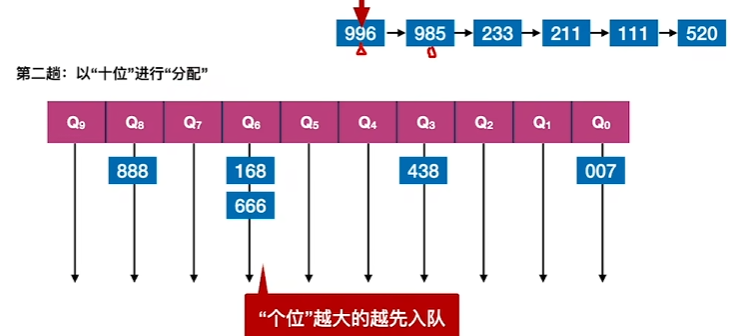
3、对数字的十位进行分配（个位数越大的越先入队）

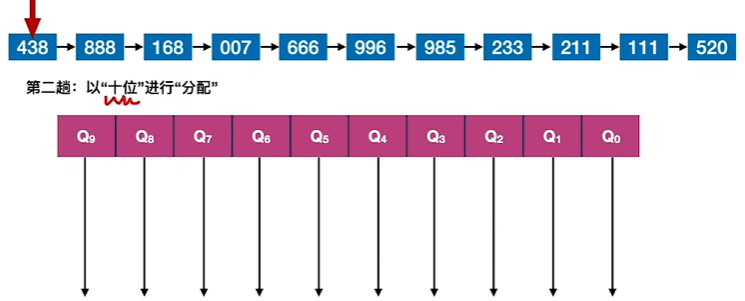
image-20241021011409685

image-20241021011454936

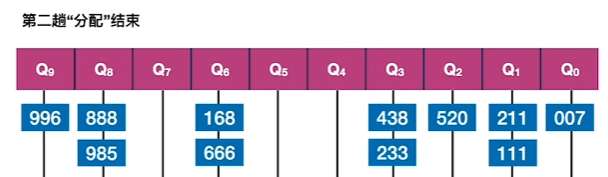
image-20241021011507073

4、对第二次分配进行收集（从前往后连成一条新的序列）

image-20241021011541271

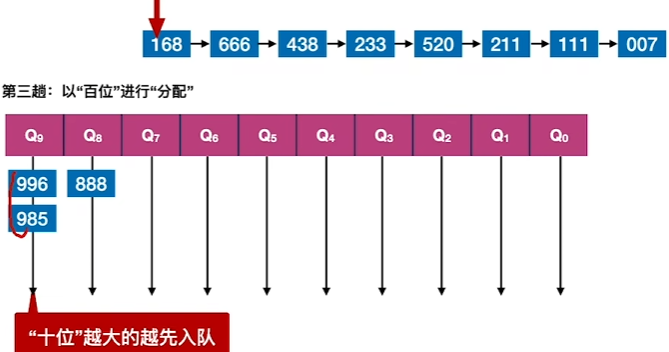
5、对数字的百位进行分配（十位数越大的越先入队）

image-20241021011621927

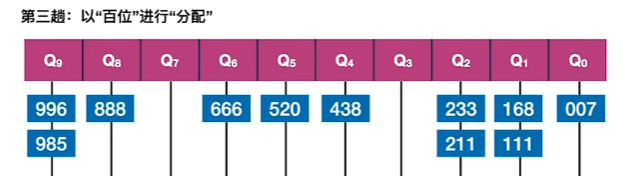
image-20241021011700397

6、对第三趟分配进行收集（从前往后连成一条新的序列）（基本已顺序排列）

image-20241021011721278

综合

image-20241021011754078

代码实现

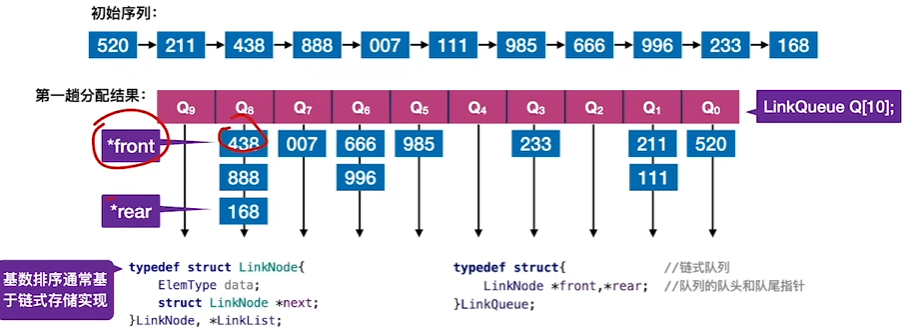
image-20241021011940922

image-20241021012150316

时间复杂度与空间复杂度

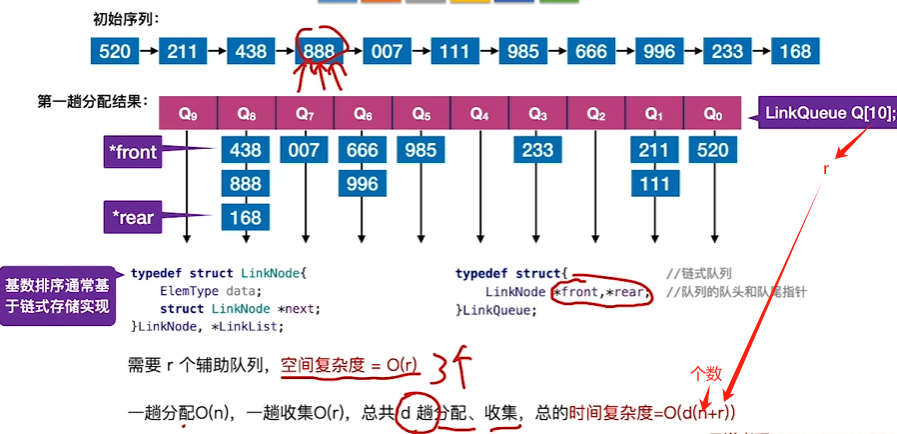
image-20241021012133248

应用角度

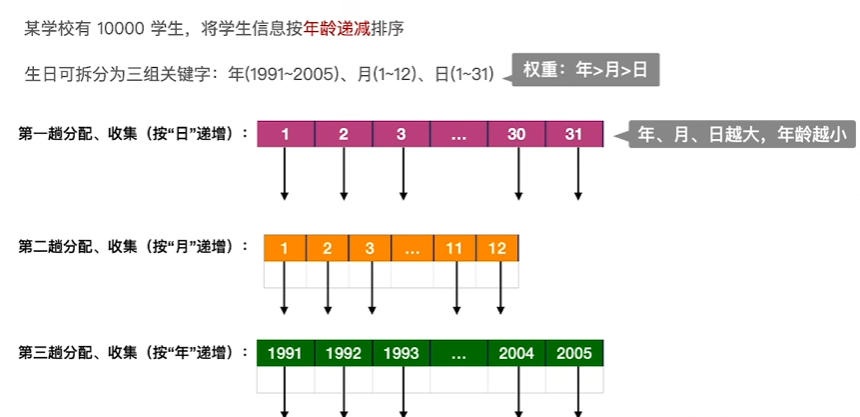
image-20241021012224293

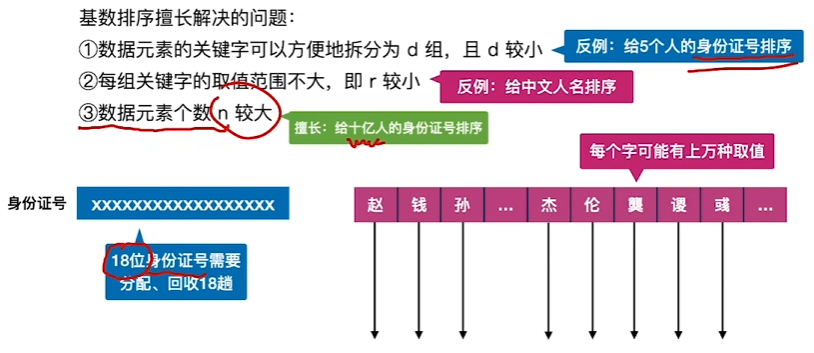
image-20241021012405059

总结

image-20241021012430015

外部排序

原理

数据元素太多，需要借助外存和内存的缓冲区进行在内存实现归并后写入外存并复写原数据

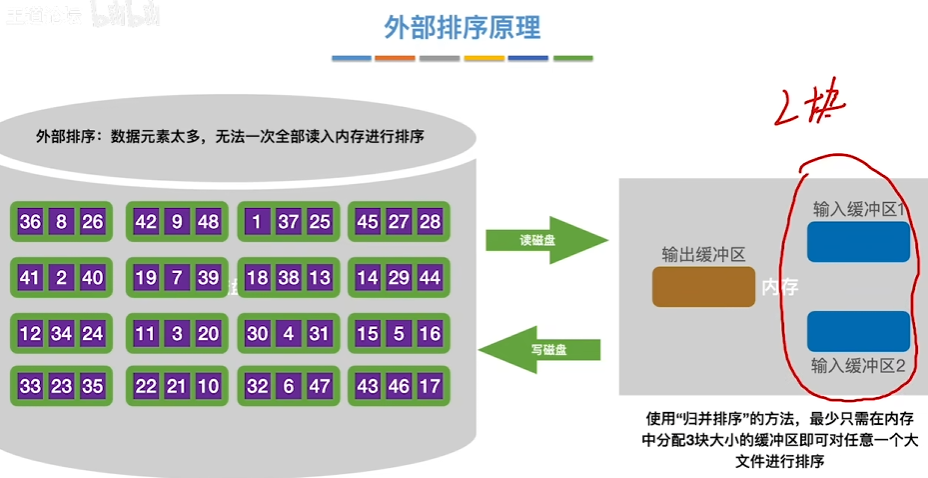
image-20241021012531897

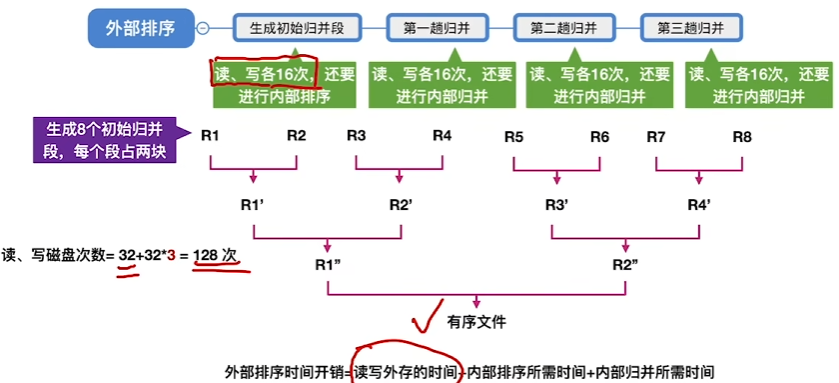
时间开销

image-20241021012647468

image-20241021012700945

优化

多路归并

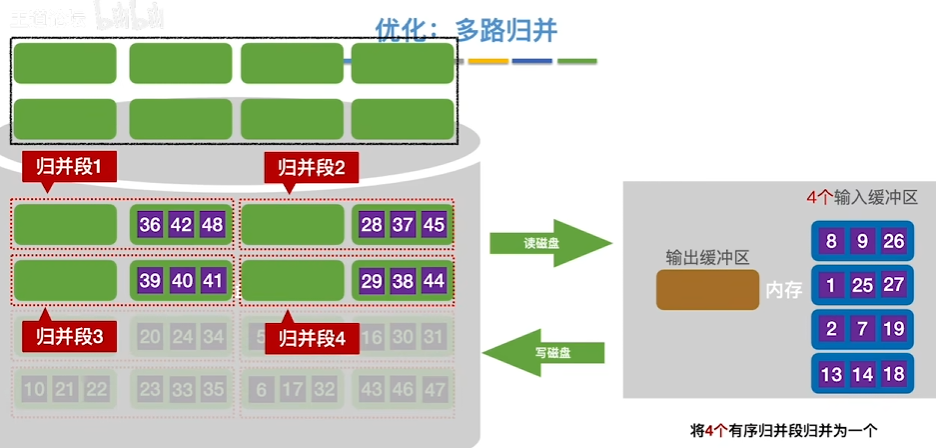
image-20241021012731274

优化：减少初始归并段

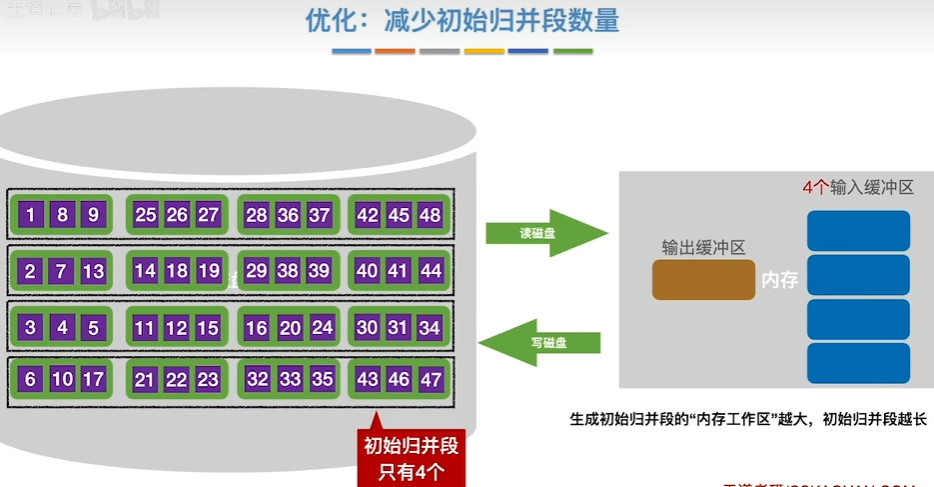
image-20241021013036872

总结

image-20241021012848089

k越大不一定越好（可通过败者树优化）

image-20241021012912761

败者树（k路归并优化）

优化原因

image-20241021013204871

定义

image-20241021013238957

原理

构建败者树

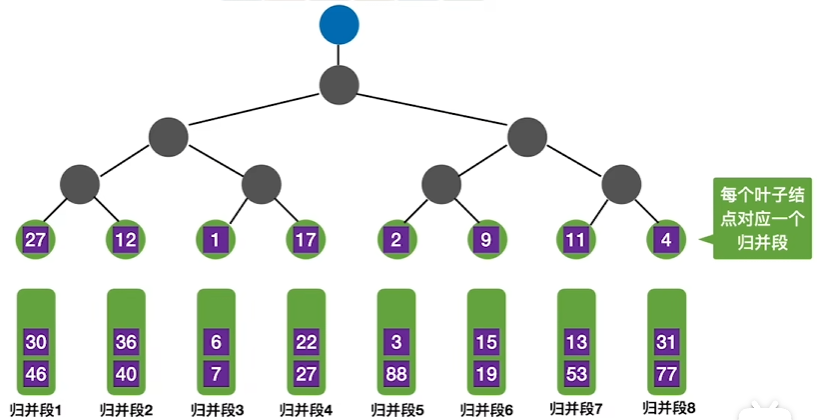
image-20241021013305989

选出每一个比赛的失败者记录其所在段号，最后的胜利者单独记录段号

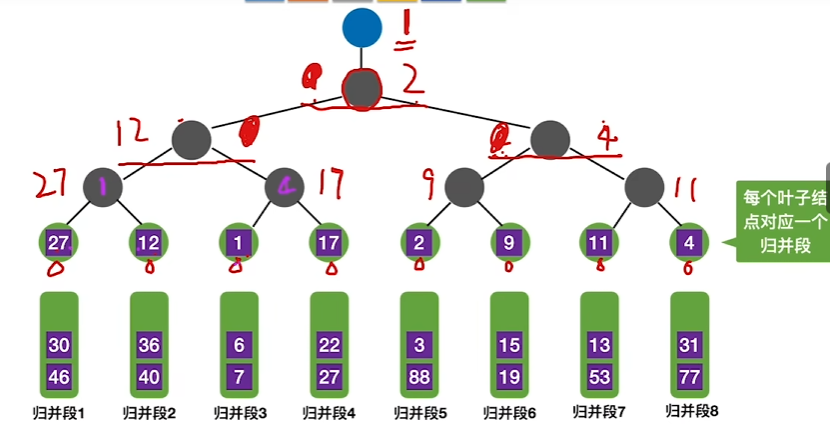
image-20241021013411626

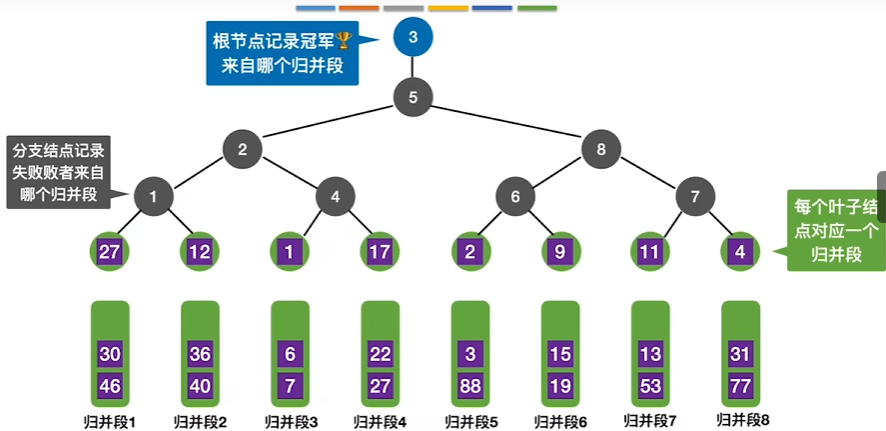
image-20241021013420385

败者树更替

归并段3的6对树中结点进行比较

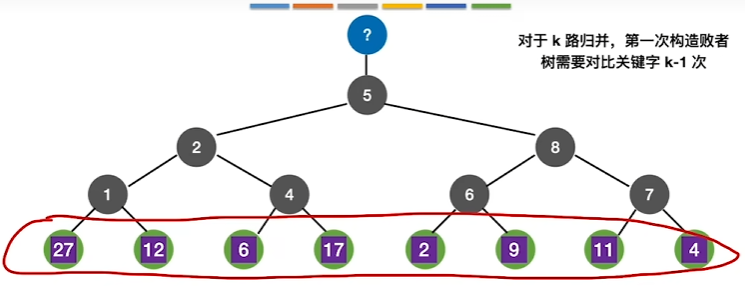
image-20241021013531710

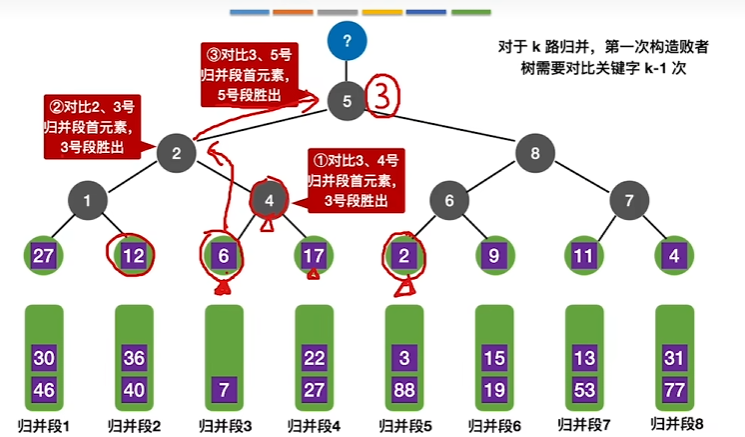
image-20241021013549704

选出最小元素

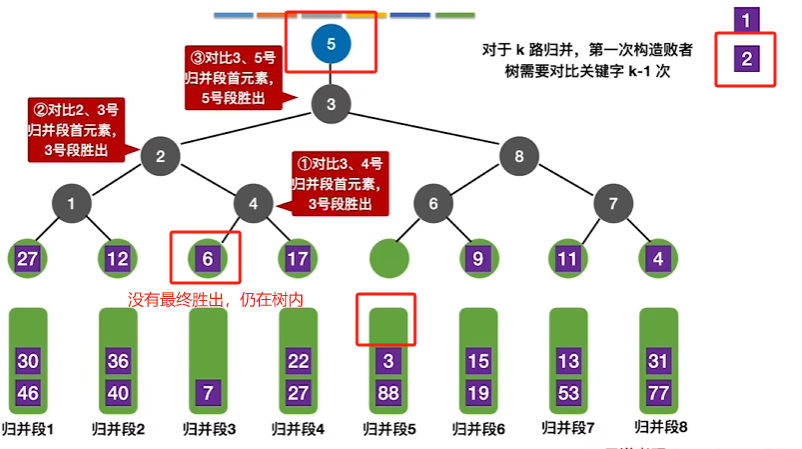
image-20241021013650245

对比次数

image-20241021013721545

总结

image-20241021013831737

置换-选择排序

原理

可以让每个初始归并段的长度超越内存工作区大小的限制

通过内存工作区，得到多个归并段

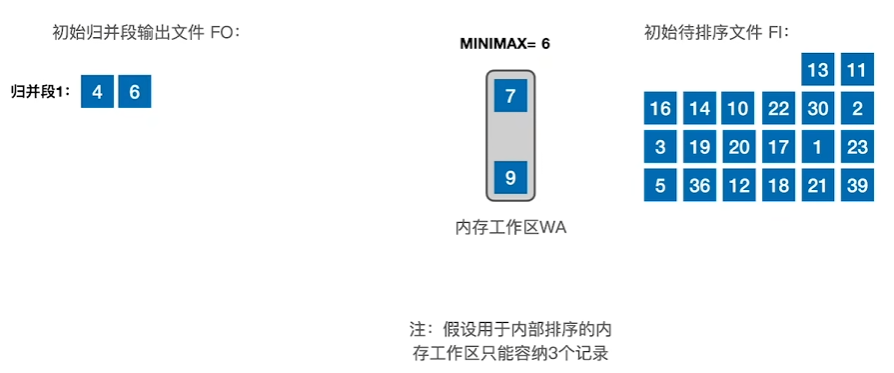
image-20241021013933263

当遇到与当前归并段不符合的顺序数时进行停留，待工作区满后开启新的归并段

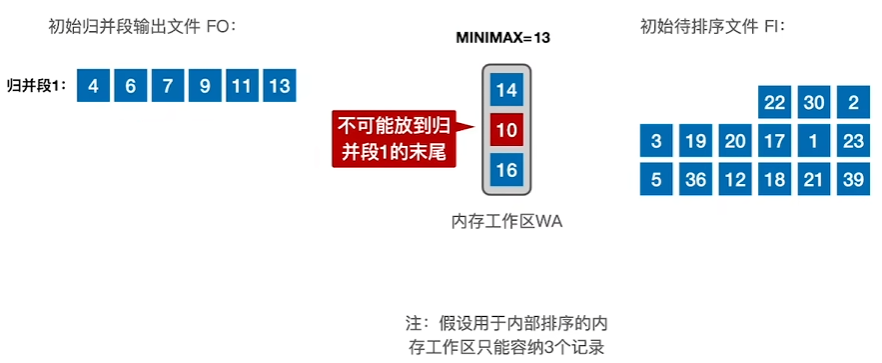
image-20241021014015038

image-20241021014023919

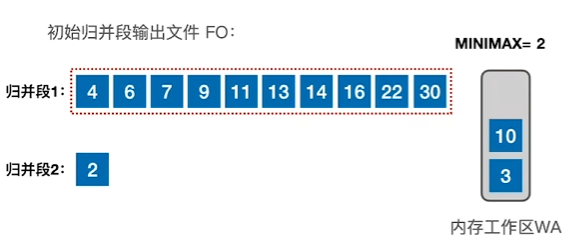
image-20241021014125443

最终得到多个归并段

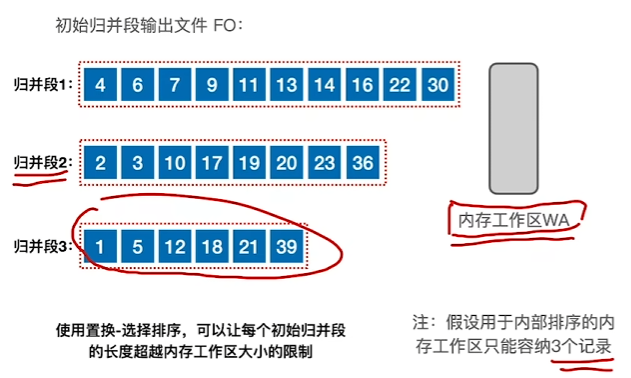
image-20241021014151408

具体文字描述

image-20241021014247281

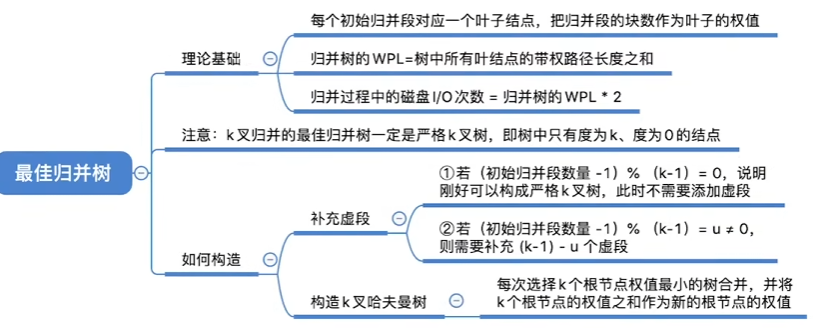
最佳归并树

定义

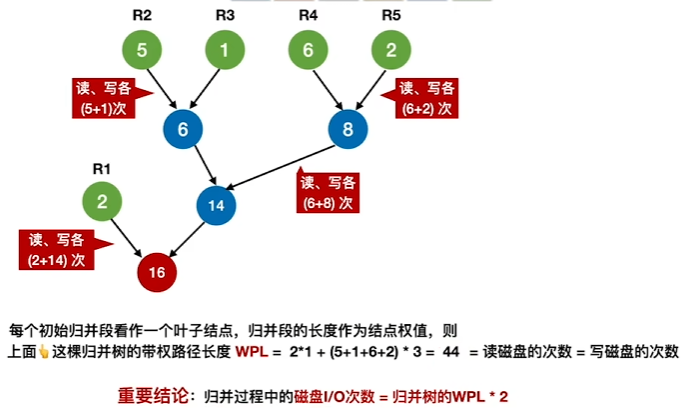
image-20241021014331011

构造最佳归并树（类哈夫曼树）

先选择最小的两个，组合后再选择两个小的，依次选择即可

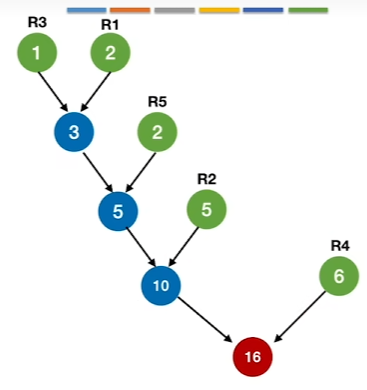
image-20241021014419470

image-20241021014502303

多路归并的注意事项

当k叉归并时，节点数不满足完美归并树，则添加虚段进行归并

image-20241021014608970

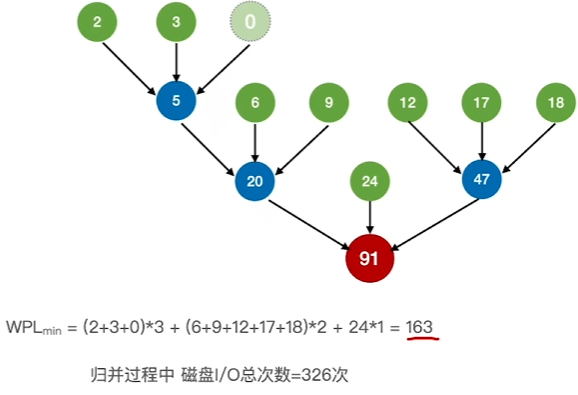
image-20241021014621779

求虚段数量

image-20241021014712343

总结

image-20241021014727008

声明

以上示例图来自王道数据结构

==本博客所有内容均为学习所用，未经允许不可进行商业转载==

  • Title: 常见简单算法归纳
  • Author: ZJ
  • Created at : 2024-10-15 00:00:00
  • Updated at : 2025-01-17 01:35:56
  • Link: https://blog.overlordzj.cn/2024/10/15/数据结构/常见算法归纳/
  • License: This work is licensed under CC BY-NC-SA 4.0.
看看这些文章吧( ૢ⁼̴̤̆ ꇴ ⁼̴̤̆ ૢ)~ෆ
关于C语言学习的部分遗漏问题解答 关于C语言学习的部分遗漏问题解答 BJDCTF2020 ZJCTF，不过如此* BJDCTF2020 ZJCTF，不过如此* C++提高编程 C++提高编程
看看这些文章吧( ૢ⁼̴̤̆ ꇴ ⁼̴̤̆ ૢ)~ෆ
关于C语言学习的部分遗漏问题解答 关于C语言学习的部分遗漏问题解答 BJDCTF2020 ZJCTF，不过如此* BJDCTF2020 ZJCTF，不过如此* C++提高编程 C++提高编程
Comments
On this page
常见简单算法归纳
  1. 前言
  2. 字符串匹配
    1. 朴素模式匹配算法（暴力解决）
      1. 原理
      2. 代码实现
      3. 时间复杂度
    2. KMP算法
      1. 原理
      2. 代码实现
      3. 求next数组
        1. 手算
        2. 机算
      4. 算法优化
    3. 比较
  3. 求最小生成树
    1. Prim算法（普里姆算法）
      1. 简单记忆：根据节点找权值
      2. 原理
      3. 理解
      4. 图实例
      5. 时间复杂度
    2. Kruskal算法（克鲁斯卡尔算法）
      1. 简单记忆：根据权值画节点
      2. 原理
      3. 理解
      4. 图示例
      5. 时间复杂度
    3. 比较
  4. 最短路径问题
    1. BFS算法（广度优先算法）
      1. 无权图
      2. 代码实现
      3. 核心思想
      4. 局限性
    2. Dijkstra算法（迪杰斯特拉算法）
      1. 图示例
      2. 代码实现
      3. 时间复杂度
      4. 局限性
    3. Floyd算法（弗洛伊德算法——动态规划）
      1. 图示例
      2. 代码实现
      3. 时间、空间复杂度
    4. 比较
  5. 查找算法与数据结构
    1. ASL概念
      1. 概念
      2. 查找成功
      3. 查找失败
    2. 顺序查找
      1. 原理
      2. 代码实现
      3. 算法优化
        1. 原理
        2. 代码实现
      4. ASL
      5. 顺序查找有序表优化
        1. 原理
        2. ASL
      6. 顺序查找被查概率不相等优化
      7. 总结
    3. 折半查找（二分查找）
      1. 原理
      2. 折半查找判定树
        1. 性质
        2. 失败结点
        3. ASL
      3. 代码实现
      4. ASL
      5. 总结
    4. 分块查找
      1. 原理
      2. ASL
        1. 已知情况
        2. 未知情况
      3. 总结
    5. BST（二叉排序树）
      1. 概念
      2. 查找操作
        1. 非递归代码实现
        2. 递归代码实现
        3. 比较
      3. 插入操作
      4. 删除操作
        1. 删除结点为叶子结点
        2. 删除结点只有一棵左子树或者右子树
        3. 删除结点有左右子树
      5. ASL
        1. 查找成功
        2. 查找失败
      6. 总结
    6. AVL（平衡二叉树）
      1. 定义
      2. 调整最小不平衡二叉树
        1. LL（左孩子右上旋）
        2. RR（右孩子左上旋）
        3. LR（左孩子的右孩子先左上旋再右上旋）
        4. RL（右孩子的左孩子先右上旋再左上旋）
        5. 代码实现
        6. 总结
      3. 平衡二叉树的删除
      4. ASL
    7. RBT（红黑树）
      1. 区别
      2. 定义
      3. 性质
      4. 时间复杂度
      5. 插入操作
      6. 总结
    8. B树
      1. 定义
      2. 特征性质
      3. 高度范围
      4. 插入操作
        1. 前提要求
        2. 过程
        3. 小总结
      5. 删除操作
        1. 过程
          1. 拉右兄弟
          2. 拉左兄弟
      6. 插入删除操作总结
    9. B+树
      1. 定义
      2. 查找
        1. 多路查找
        2. 顺序查找
      3. 对比B树
        1. 关键字对应分叉不同
        2. 节点关键字范围不同
        3. 叶子结点与关键字的关系
        4. 节点作用
        5. 存储本质区别
      4. 总结对比
    10. 散列查找（空间换时间）
      1. 概念
      2. 散列函数
      3. ASL
      4. 装填因子
      5. 常见散列函数设计方法（哈希函数）
        1. 除留余数法
        2. 直接定址法
        3. 数字分析法
        4. 平方取中法
      6. 处理冲突方法
        1. 拉链法
        2. 开放定址法
          1. 线性探测法
          2. 平方探测法
          3. 伪随机序列法
        3. 再散列法（再哈希法）
      7. 总结
  6. 排序算法与数据结构
    1. 插入排序
      1. 原理
      2. 代码实现
      3. 时间复杂度
      4. 优化——折半查找
        1. 优化代码实现
        2. 时间复杂度
      5. 总结
    2. 希尔排序
      1. 定义
      2. 原理
      3. 代码实现
      4. 时间复杂度与空间复杂度
      5. 稳定性与适用性
      6. 总结
    3. 交换排序
      1. 冒泡排序
        1. 原理
        2. 算法实现
        3. 时间复杂度与空间复杂度
        4. 总结
      2. 快速排序（最快）
        1. 定义
        2. 原理
        3. 算法实现
        4. 时间复杂度与空间复杂度
        5. 总结
    4. 选择排序
      1. 简单选择排序
        1. 定义
        2. 原理
        3. 代码实现
        4. 时间复杂度与空间复杂度
        5. 总结
      2. 堆排序
        1. 定义堆
        2. 建立大根堆
          1. 代码实现
          2. 堆的插入与删除
        3. 基于大根堆排序
          1. 原理
          2. 代码实现
        4. 时间复杂度与空间复杂度
        5. 总结
    5. 归并排序
      1. 定义
      2. 原理（二路）
      3. 代码实现
        1. 完整代码（递归）
      4. 时间复杂度与空间复杂度
      5. 总结
    6. 基数排序
      1. 定义
      2. 原理
      3. 代码实现
      4. 时间复杂度与空间复杂度
      5. 应用角度
      6. 总结
    7. 外部排序
      1. 原理
      2. 时间开销
      3. 优化
        1. 多路归并
        2. 优化：减少初始归并段
        3. 总结
      4. 败者树（k路归并优化）
        1. 优化原因
        2. 定义
        3. 原理
        4. 对比次数
      5. 总结
    8. 置换-选择排序
      1. 原理
        1. 具体文字描述
    9. 最佳归并树
      1. 定义
      2. 构造最佳归并树（类哈夫曼树）
      3. 多路归并的注意事项
        1. 求虚段数量
      4. 总结
  7. 声明